^Top

Morphic Polytopes

Posted 30 Aug 2019. Last updated 3 Feb 2024.

Contents

Around the turn of the millennium I began to realise the mess which is polyhedron theory today and set out to try and find something better. What is emerging from this work is a foundational theory of polygons, polyhedra and higher-dimensional polytopes which I call morphic theory. It progressed slowly and only in 2015 was I able to firm it up enough to give it a sensible outline, but it was still only an outline and I have continued to be distracted by other things, making only slow progress since then. So, rather than wait any longer, a few years ago I set out as much of it as I could and have been adding stuff as I find the time. The theory now seems to be shaping up quite well.

But I have to be careful. I am no more above the odd gross blunder than anybody else, which has obliged me to rework aspects of the theory from time to time. Branko Grünbaum spotted my worst one in a draft paper, and a few years later I was able to repay him by spotting nearly as gross an example in one of his own drafts. Meanwhile one of Poincaré's foundational conjectures (see below), the ability to decompose any given manifold into a definite set of simple pieces, has in the 21st century been proved false in four dimensions (and only for certain manifolds in four dimensions) and so despite it being true everywhere else, its applicability must be treated with caution.

Part I : The Problem

Origins

Our first mathematical writings on plane polygons and solid polyhedra come from classical Greek authors such as Plato and Archimedes. While hollow bronze dodecahedra were made by the Etruscan ancestors of Rome, the geometers came to treat polyhedra a solid bodies. So it remained for the next thousand years and more, and we still talk of the Platonic and Archimedean solids today.

When Gottfried Leibniz conceived of an algebraic analysis of position, his analysis situs in the 17th century, he envisaged a new mathematical discipline concerned only with the innate characteristics of structural forms without any reference to quantitative measurements. Leonhard Euler delivered its first stirrings with his famous polyhedron formula V − E + F = 2 and its close correspondence with planar graphs. He called his discipline stereometry but while the name did not stick, his ideas did. Two visually distinct polyhedra with similar connectivity of faces, etc. came to be regarded essentially as different examples of a common underlying form, for example a rectangular box or a sloping parallelepiped is in essence the same as a cube. Henri Poincaré later developed analysis situs hugely, applying it to general surfaces or manifolds. One of his chief tools remained Euler's decomposition of a topological object or manifold into pieces – polygons, polyhedra and so forth – maintaining the foundational link between the two disciplines. Thus, for example, the surface of a polyhedron could be seen as a polygonal decomposition of its associated two-dimensional surface manifold. Poincaré's most innovative and powerful methods also decomposed the entire body of the polyhedron into chains of tetrahedra – three-dimensional simplices – and treating the whole solid as a bounded three-dimensional manifold. In the 20th Century the field became known as topology and, through the algebraic formulations of Emmy Noethe and others, came to play a fundamental role in much of modern mathematics. Much of the century was spent proving Poincaré's huge outpouring of ideas – the famous conjecture which bears his name was not proved by Gregor Perelman (and another conjecture proved false) until the dawn of the 21st century. Incidence complexes, and especially CW complexes, arose in algebraic topology as formalisations of Poincaré's chains and related structures.

From the moment Euler noticed the equivalence with graphs, the focus of polyhedron theory had moved more and more to the surface until the polyhedron became defined as its surface and its body discarded as of no significance. In the latter half of the 20th Century Bonnie Stewart studied toroidal polyhedra, seemingly for the first time actually defining his polyhedra as topological surfaces.[8]

The theoretical significance of Stewart's topological definition was largely lost on his mainstream contemporaries. They were busy developing more fashionable set-theoretic and combinatorial ideas. At that time set theory was touted as the universal foundation of all mathematics and even of philosophical logic and all rational thought; it has since failed to live up to expectations. Among the fans of set theory was Branko Grünbaum, who from the start highlighted the continuous geometric transformations or morphing between examples of a given structural form. This notion of plasticity had always been key to topology (and remains key to morphic theory) and, crucially for Grünbaum, it also provided a rationale for preserving the abstract combinatorial structure of the associated set of points, lines and so forth, even when individual elements became geometrically superimposed.

Other abstract theorists too were not interested in the exact shape of a figure but only in its "polyhedron-ness" in terms of connected faces and so forth which were incident with each other. In particular Danzer, McMullen and Schulte to some extent paralleled the work of Grünbaum in this field. But they went further, eventually coming up with a rigorous description of such abstract polyhedra in terms of a partially-ordered set (poset) of elements corresponding to the faces, edges and vertices, as part of a more general model of abstract polytopes in two and higher dimensions. Moreover such a polytope was effectively a set of sets, the Holy Grail of the set evangelists. These subsets comprised cardinal-1 sets each containing a vertex point, cardinal-2 point sets or point pairs (as edges) and cyclically ordered sets of point pairs (as faces), and also including the whole set (since every set is a subset of itself) as a maximal element and the empty set (also a subset of every set) as a minimal element. These subsets or elements were partially ordered via a ranking hierarchy and a pairwise incidence relation. The resulting abstract structures belonged to the more general class of incidence complexes. Their purely combinatorial connectivity could if desired be "realized" as a geometric polyhedron by injecting it into some ordinary geometric space.

Up to solids in three dimensions, modern abstract theory appears consistent with the traditional topological approach via decomposition and CW complexes. However some argue that the difference in conceptual bases still causes problems.[1] Beyond that, in four dimensions and above, the abstract approach is already acknowledged to allow more general structures which topologists would throw up their hands at in horror. For example a piece of a topological decomposition must be a simple topological ball, while an equivalent "j-face" of an abstract polytope may be say a toroid or a projective plane. In this, certain thorny examples of apparently paradoxical polyhedra have led me to follow the set theorists towards greater generalization. But more of that later. Moreover the process of realization was never pinned down, it has remained a kind of woolly rag-bag into which all the old inconsistencies and disagreements have been carelessly stuffed. Abstract theory has provided a useful algebraic toolset but has probably introduced more conceptual difficulties than it has resolved.

Essentially I have sought a more satisfactory general theory by following Stewart's approach another step back towards Poincaré's, considering not only the surface but also the interior as a topological object in its own right, a bounded manifold. For example a beach ball is a hollow sphere, a 2-manifold, while a bowling ball is a solid, a bounded 3-manifold. Topology is sometimes aptly described as "rubber-sheet geometry", ignoring lengths and angles (except as aids to analysis) and just considering the underlying structural form or morphology. That is pretty much how I have approached polyhedra and so I call my ideas morphic theory.

From the morphic standpoint, the various properties of a geometric polyhedron arise from several distinct disciplines or layers of understanding:

Broadly speaking, we can see these layers as a hierarchy of increasing restrictions on a polyhedral form. Alternatively, reading up from the bottom we may see it as a progressive relaxation of conditions and generalisation of the figure. But this is an over-simplification; these approaches are in many respects independent and their relationships are not always obvious (hence much of the historical inconsistency and confusion).

A rubber sheet has a precisely connected interior. But as already mentioned, abstract decompositions go beyond rubber sheets to shapes whose interiors are not even defined. Morphic theory bridges this gap by – but I will introduce that through a motivational example.

Motivational example

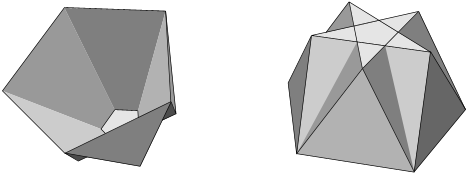
The pentagonal cuploid

Although my original motivation arose from my studies on stellating the icosahedron, the family of polyhedra known as cuploids provide a more convenient example. The pentagonal cuploid shown has side walls formed of five intersecting squares and five equilateral triangles. Its base is a star pentagon. These polyhedra have a curiously paradoxical property. They have the superficial appearance of toroids, except that one end of the central hole is closed off by a membrane. Or is it? The membrane, typically the central region of a star polygon, is wound twice around its central point, making it appear to be two layers thick. Arthur Cayley pointed out how we can treat such layers of a self-intersecting polyhedron as surrounding a dense interior, so passing through two layers should give a density change across them of 2.[3] Except, in the case of a cuploid, both sides are outside the polyhedron so the density on both sides is zero and the net change across the layers, the difference between them, is therefore 0 − 0 = 0. One might suggest that the two layers are oriented oppositely, giving the true change across the membrane as 1 − 1 = 0. However topologically a cuploid is a projective plane, the simplest non-orientable manifold. Non-orientable densities do not add consistently in the same way as orientable ones, but can achieve no more than a modulo 2 count, according to whether the number of layers is odd or even, giving: 1 + 1 [modulo 2] = 0.

A second paradox arises when we ask whether this zero-change membrane is therefore a membrane at all. If there is no change in density across it, then surely it cannot exist and there must be a hole there. But a hole would open up a through-hole from one end of the polyhedron to the other, changing it to a different manifold, a non-orientable toroid known as the Klein bottle. Worse, the star polygon would no longer be a topological disc, one of the key requirements for (what I will call in this context) a proper decomposition, meaning that the figure was not even a polyhedron any more. Whatever way we try to resolve the paradox, we run into trouble.

Dualising the cuploid rubs in the paradoxical nature even more. A dual is typically obtained by reciprocating the polyhedron about a concentric sphere (for asymmetric polyhedra we define the centre as the mean position of its vertices). For a cuploid this yields a hollow pyramid-like form which I call a keratinoid or cornoid, because it is reminiscent of an old-style drinking horn in the same way that a cuploid is reminiscent of a drinking cup.

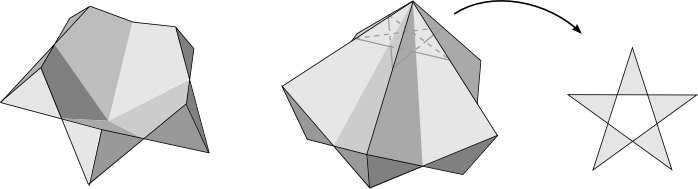
The pentagonal cornoid, with vertex figure of apex

The vertex figure of its apex, loosely speaking the section revealed when the vertex is cut off, is without question a star pentagon with a hollow central region. Like the cuploid, the cornoid is topologically a non-orientable projective plane. This requires that the surface be connected at its apex, because otherwise it would correspond to the open base and preserve the Klein bottle. How, then, can we have a connected vertex whose vertex figure is hollow? How do we even define a hollow star pentagon, as traditional topology ignores the hole, definitions based on the bounding circuit ignore the whole interior, and abstract theory ignores the entire geometry. Is it a mutilated solid pentagon, or what?

In order to resolve such dilemmas, morphic theory offers a different approach (whether we regard it as novel, or as harking back to 19th century suggestions banished by Poincaré and his ilk, is a matter I will not pass judgement on). One may consider any polygon, which forms a face or "2-cell" of a polyhedron, as a bounded manifold in its own right, with the boundary decomposed into a polygonal circuit of edges and vertices.

The nature of the cuploid surface, as a topological decomposition of the projective plane, requires that the base be treated as a topological disc. In the example, the pentagon is first twisted up and flattened down to make a star figure with a two-layered core, which we may call a Cayley star. This core forms the base of the cuploid. The morphing process, as illustrated, reveals a feature which is seldom noticed. As a model of the projective plane, the cuploid is said to be immersed in ordinary space. When the pentagon is twisted round and flattened, it makes a double-circuit - an angle of 4π or 720° - around a point. This double-wound point forms a singularity in the otherwise smooth geometry of the surface. To preserve symmetry the point is pushed to the centre of the pentagon, shown as P in the diagram. In morphic theory, every Cayley polygon must have such a point.

Morphing a disc-like pentagon into a star

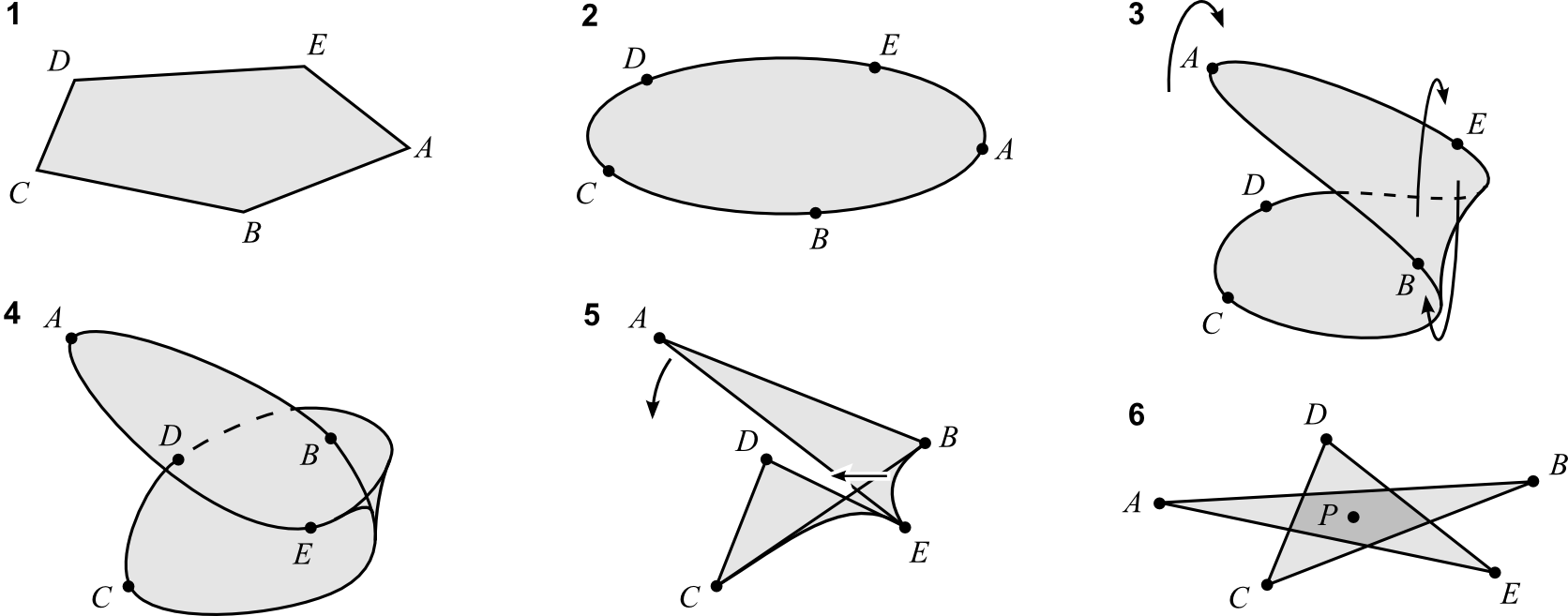
Turning now to the vertex figure of the cornoid apex, perhaps the first thing to do is to define it fully in terms of its topological properties. Clearly it drops the usual insistence that the piece must be disc-like. This is however perfectly consistent with abstract theory. Noting that topologically a projective plane is a glued-together disc and Möbius band, we here choose the Möbius band. (I prefer the less common English-language description as a "band" because it implies a closed loop whereas "strip", as generally used, may also refer to a flat length with two ends. It is also a band in German, the native language of its discoverers August Möbius and Johann Listing. "Strip" is thus a mistranslation, which it is high time was put right). The illustration below shows how such a band can also be bounded by a polygonal circuit and squashed down into a star polygon. However this time it has a hole through the middle. This matches the polygon seen in the vertex figure and may serve as its definition.

Morphing a Möbius band into a star

The cornoid is, like the cuploid, an immersion of the projective plane in some 3-space. Its apex is a singularity where the hole through the centre ends and the surface connects across. Its vertex figure is now seen to reflect the non-orientability of the surface by being itself non-orientable.

The resolution of the original paradox is now straight forward. Because the cuploid surface is non-orientable, the star pentagon at its base inherits this property even though it may be locally orientable. Since it is double-layered it has density [modulo 2] = 0. Thus, the density value is no longer expected to match the layer count; Cayley's method, which equates the two, is applicable only to the special case of orientable polyhedra. The cornoid paradox is resolved by recognising the existence of a distinct star pentagon made from a Möbius band. Neither it nor its dual face can obeys Cayley density rule, because both are non-orientable.

Topological manifolds

Topological analysis originated in the idea of decomposing a smooth manifold into pieces (and then analysing the way these pieces form chains to cover the manifold). The pieces must all meet at their corners, with no corner of one piece slipping along the edge of another. For a two-dimensional surface this is equivalent to drawing a graph or constructing a polyhedron composed of polygons. In general, a polytope can be understood as a graph drawn on, or embedded in, the associated topological manifold. Such a manifold is unbounded and usually finite, although tilings and sponges are sometimes treated as infinite polytopes or apeirotopes. As a graph, it forms what might be called a "proper" topological decomposition of a manifold.

It is fundamental to both graph theory and topological analysis that all the pieces of a topological decomposition, i.e. elements of the graph, should be simple topological balls. That is to say, the Jordan curve theorem holds and any closed loop drawn on the piece may be shrunk to a point. A disc is a 2-ball, a solid block a 3-ball, and so on. We also include the line segment as a 1-ball and the point as a 0-ball. On a polyhedron, a convex face is a 2-ball. As such the polytope is also an example of what topologists call a chain, and also a CW complex.

The cuploid example has shown the necessity to include the interior of a polygon in its full definition. Generalising this object lesson, we may understand that such a polytope has an interior or body and thus comprises what topologists call an n-manifold with boundary, the latter being its bounding surface. The surface itself is a closed unbounded (n−1)-manifold. While this surface manifold has often been identified since the 19th century as the polytope itself, this was not originally the case and Poincaré's work on decomposition encompassed the entire bounded manifold or solid, and much analytical topology is still based on this understanding. Topology is thus well able to deal with bounded manifolds, they present no problem in this respect.

From this viewpoint the bounding surface, intersections of half-spaces, point sets and other such approaches are seen as particular aspects which a geometer may choose to focus on and not as general definitions of a polytope.

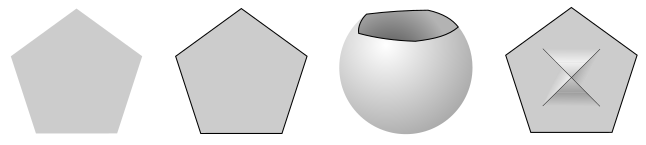
Four 2-manifolds. The first is open, i.e. excludes its boundary. The remaining three
are all closed or bounded; the middle two are topological discs, the last has
a cross-cap which makes it a Möbius band.

If the last two 2-manifolds illustrated were zippered or glued together along their boundaries, the resulting 2-manifold without boundary would be a projective plane (i.e. a projective 2-space). This gives some idea of the importance which topologists attach to boundaries and to the characteristics of the manifolds they bound.

However, the hollow star pentagon is a Möbius band and not a disc. The interior no longer supports the Jordan curve theorem and can no longer be decomposed into a chain or CW complex. Are we forced to conclude that not all vertex figures are valid polygons? This is where the cornoid is in danger of parting company with Poincaré's topological rigour. But it poses no problem for abstract theory.

Abstraction and realization

An abstract polytope is a purely set-theoretic construct which captures the overall structure of its elements – vertices, edges, faces, etc. – and their connections to each other. The elements are ranked in order of their dimension, with vertices in rank 0, edges in rank 1 and so on. A further partial ordering is provided by the incidence relations between elements of adjacent rank. In the traditional set diagram, known as a Hasse diagram, the incidences are shown as joining lines. The rules for the arrangement of incidences are rigorously restricted; in this, an abstract polytope is a particular example of the more general incidence complex. In Polytopes - Abstract and Real, Johnson describes these restrictions as monal (each element only occurs once), dyadic (conforming to the diamond condition) and properly connected (no subset is a polytope of equal dimension). The description which follows is somewhat simplified but it is adequate here; some further discussion may be found in A Critique of Abstract Polytopes.

The illustration shows Hasse diagrams of the four simplest abstract polytope structures. The null or empty element A is just a simple placeholder and may be thought of as a kind of equivalent to the empty set or the number 0 in arithmetic. Its rank is one less than 0, or −1. As a standalone element it comprises the null polytope or nullon. The 0-polytope or monon B comprises a point which is incident only with the null element. A point has dimension or rank 0, with the null element beneath it therefore given the dimension −1. Above these the 1-polytope or ditelon comprises a line segment D incident with two points or 0-polytopes, B and C. The simplest 2-polytope or polygon is the digon.

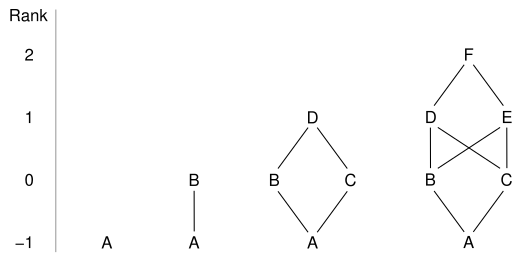
Hasse diagrams respectively of the nullon, monon, ditelon and digon.
A is the null element, B and C correspond to vertex points, D and E
to line segments and F to a plane region

An abstract polyhedron must also satisfy some other conditions, most significantly that a line is incident with only two endpoints, an edge of a polyhedron with only two faces, and so on. This is known as the diamond condition, owing to the characteristic presence of diamond shapes in the Hasse diagram. Such a set is said to be dyadic. The ditelon is the simplest structure able to show this condition, with the monon and nullon being somewhat honorary polytopes. Several diamonds can be traced in the diagram of the dihedron. The digon and dihedron are degenerate in conventional Euclidean geometry but finite in many non-Euclidean situations. Although these four figures are often excluded in working definitions of a polytope, they are important in the procedures used for topological analysis and graph theory as well as in abstract theory.

An abstract polytope is a purely set-theoretic construct. It has no geometric form until mapped or injected into some containing space, a process known as realization. However the form of the resulting geometrical figure need not look much like the abstract structure. The hour-glass-like polyhedron below has four cross-quadrilateral faces and four edges geometrically incident at a false vertex but not structurally incident, which is therefore said to render it "unfaithful." The accurate cube is a "faithful" realization.

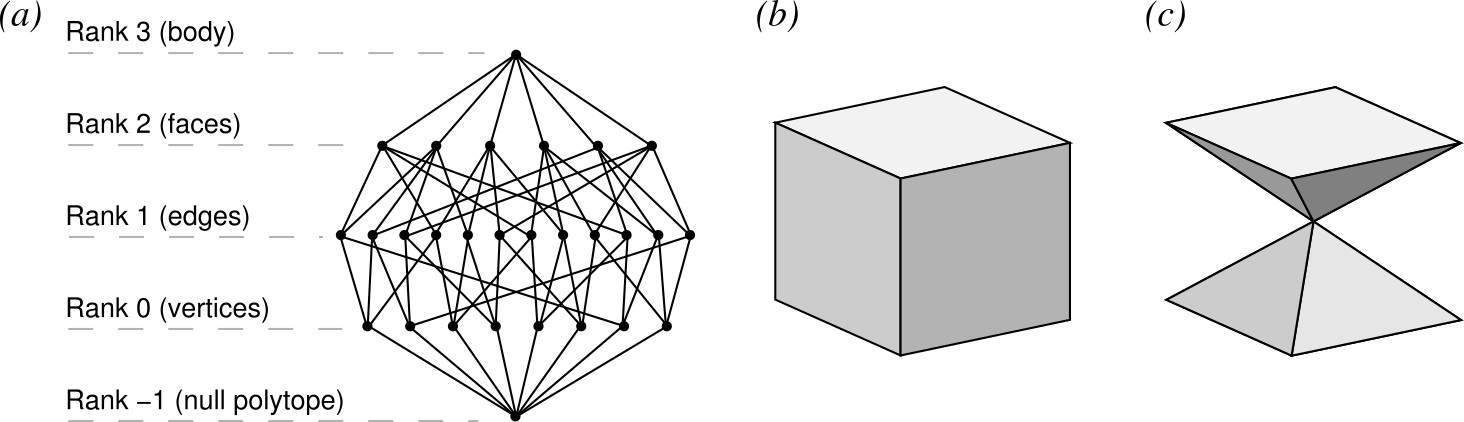
Hasse diagram (a) and two realizations (b), (c) of the abstract cube

The awkwardness of introducing unfaithfulness is compounded by valid abstract polytopes which have no unique associated manifold because, unlike graphs or CW complexes, their j-faces are not necessarily simple topological j-spheres and so the usual topological analysis of the surface can not be applied. What does faithfulness mean for these polytopes? More generally, which mappings of which polytopes preserve faithfulness and which do not? The questions mean nothing while faithfulness remains undefined. Indeed the whole idea of realization has turned out to be just a woolly rag-bag of all the problems, old and new, that had grown up over the years and abstract theory had hoped to resolve.

Faithfulness and tidiness

Abstract theory's original, vague idea of realization as some kind of mapping turned out to be too broad and undefined for all such realizations to meet their aspirations. For example if every element of a complicated structure is mapped onto a single point in the containing psace, this is not helpful in developing an understanding of the polytope. Realizations therefore became judged by an extra criterion of "faithfulness." But there is no universal definition of what a faithful realization is either; commonly a geometer might want abstract symmetries to be retained as geometric symmetries and no elements to overlap or superimpose over each other, while others might also demand that the realization of any topological ball be convex or that no elements intersect at all (a bijection). What one geometer finds faithful, another may not, while a given polyhedron may have a faithful realization for one geometer but none for another. For example to some the cuploid is unfaithful because it self-intersects, while say the hemicube is even worse because it cannot be given flat faces without elements coinciding and its symmetry being broken. It may be possible to realize the figure faithfully in one containing space but not in another, for example the hemicube may be realized as a regular tiling of the projective plane but in Euclidean space will always be curved or otherwise degenerate.

From the abstract point of view, such geometric properties of any realization are wholly irrelevant. Faithfulness is an afterthought, to be added if desired in whatever form might suit the purpose of some concrete geometer.

Before I came across abstract theory, in my own studies of stellations and facettings I had developed a concept of geometric "tidiness", which is similarly defined according to one's area of interest and which the present context leads me to describe as the geometric quality necessary for the figure to achieve faithfulness to the abstract. That is to say, a tidy geometric polytope is one which is faithful to its abstract structure. The distinction between faithfulness and tidiness is thus one of approach; from the geometrical point of view the figure is tidy, in the abstract view it is faithful. Put succinctly, a faithful realization is a tidy geometric polytope, and vice versa. Some further discussion may be found in Polytopes: Degeneracy and Untidiness, another work in progress.

Part II : Morphic Theory

The morphic synthesis

Morphic theory is my attempt at an overarching theoretical model of polyhedra and polytopes generally, in which all these disparate traditions may be found a home and the inconsistencies between them placed in context.

As an initial definition one might say that a morphic 0-polytope is a point and, for n > 0, a morphic n-polytope is a bounded, smooth n-manifold whose boundary is decomposed piecewise into (n−1) polytopes.

This is essentially a topological definition. We understand that the boundary of a 1-manifold is a point pair. While its interior is of necessity a 1-ball, we do not impose the usual condition that the pieces of all dimensions be balls.

At least in origin, topology deals in rubber sheets which already exist in ordinary space but have no definite size or shape. We may maintain the link between topology and graph theory by defining specifically the boundary of a polytope as the graph embedded in the associated manifold. However, to define the polytope fully, the topology of its body must also be defined. There is as yet no notion of a metric, of measurements, of things like size, local curvature or angles. This half-formed, rubber ghost of a solid, with its surface decomposed into vaguely-shaped but precisely-joined polygons, and deformed by known twists and holes, is an example of a morphic polyhedron or, generalized to any number of dimensions, a morphic polytope.

These more general structures are just those admitted by abstract theory. A more general definition of a morphic polytope in this vein would be an abstract n-polytope mapped bijectively onto a bounded n-manifold such that the ranking and incidences are preserved.

Thus, from the abstract point of view, morphic theory may be understood as a theory of realization. It divides the full geometric realization into a two-step process:

  1. Interpretation. The various elements of the abstract polyhedron are first interpreted as some kind of geometric entity. They could famously be interpreted as tables, chairs and beer mugs (as would be entirely legitimate), but that would not suit the conventional geometer. The original combinatorial idea of a set of subsets has proved unnecessary and has been abandoned in the most highly abstracted theories, with such subsets being understood as certain "sections" (or subposets or subtopes) of the polytope and quite distinct from the actual elements. Such set-of-sets models may be seen as alternative interpretations of the foundational abstract form. The infinite lines and planes to be found in the theory of configurations (and the more esoteric complex lines of complex polytopes) are consistent with abstract theory, but they are not consistent with the decomposition of a smooth manifold. The morphic interpretation treats the main elements strictly as pieces of a smooth manifold according to their dimension, with the maximal element as the interior or body and the abstract incidence relation deemed to be a geometric incidence or connectivity between adjacent pieces.
  2. Concretization. The containing space, together with any metric it may have, must now be defined and the morphic polyhedron injected into it via a second, concrete mapping. The result is a geometric polytope. Because a morphic polytope is already in some fundamental sense geometric (in the same way as projective geometry), a particular example of such an immersion is called here a concrete polytope. To aid in this the polyhedral manifold (i.e. the interpretation) may also be given an innate metric of its own, in which case the mapping between the two metrics will also need to be defined. The geometric alignment, overlapping or coincidence of distinct elements are in principle allowed, while the pieces retain their individual structural identities.

This approach to realization leads us to a taxonomy of polytopes and related constructs along the lines shown in the diagram. The dyadic property is Johnson's term for the diamond condition. Some of the longstanding names for certain constructs appear to bear little logical relation to the main taxonomy; students coming later to the field can be forgiven for becoming confused over them.

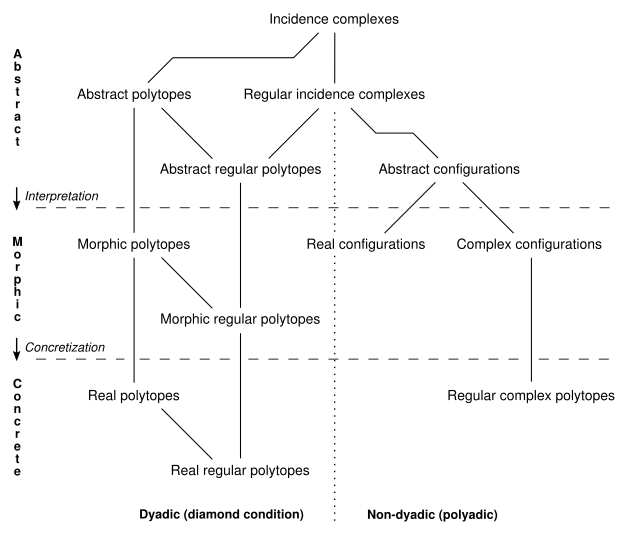
A partial taxonomy of incidence complexes

Morphic theory understands or interprets the abstract partial ordering in a manner consistent with the topological and graph-theoretic approaches (this is not represented in the above taxonomy). However even with the body defined, strict topological decompositions are only a part of the story. Following the abstract model, morphic 4-polytopes and higher admit more general decompositions which topology is ill-equipped to study.

Non-simple (anaploid) pieces

A fundamental difference has arisen between the topological and abstract structures in the above discussion, in that the abstract construction of the polytope need not be a topologically rigorous one after the manner of Poincaré (topologists might say that it is not equivalent to a chain complex or even a CW complex, graph theorists would be similarly sniffy). This appears to be the root issue in a high-profile argument which blew up in 1994.[1] However the morphic approach demands that, despite accepting the abstract position, topological rigour must still somehow be accommodated.

The cuploid and cornoid introduced above might at first sight appear to compound the problem. In its recognition of two distinct yet valid star pentagons, the discussion goes beyond both conventional topology and abstract set theory. Where the Möbius pentagon is flatly inconsistent with topological models, the issue with the abstract formulation is merely one of realization. Yet, at the same time, it generalises the standard topological approach in a way which creates a new and self-consistent model.

Many non-convex polyhedra have surfaces and interiors which are not simple, i.e. they are not topological spheres or balls. This is what led to the first extension of Euler's formula, to include polyhedra with toroidal holes or handles and non-orientable twists. The cuploid is one example, Stewart's toroids provide another. I shal call such topologically non-simple objects anaploid from the classical Greek απλους (aplois) meaning simple.

Where topology demands that any piece of a decomposition be a topological ball, abstract theory makes no such demand and allows us to join together pieces of more general shapes without restriction, to form a higher polytope. For example polyhedral projective planes, such as the cuploids and cornoids, may be used to construct what are known as projective polytopes. Abstractly, these are perfectly respectable. But they are not graphs or CW complexes. Even if the pieces of a polytope do conform, its body may be anaploid. So, when itself used as a cell in a higher polytope, the figure does not obey the higher-dimensional analogues and extensions of Euler's polyhedron formula, and its topology cannot be expressed analytically and unambiguously. For example if we substitute a hollow Möbius star for the base of the pentagonal cuploid, we obtain a surface which is topologically a Klein bottle instead of a projective plane, although its sum of V − E + F does not change. It is still a valid abstract polyhedron but it is no longer a proper topological decomposition of either manifold. Thus, the abstract departure from simple balls means that there is in general no longer a unique manifold associated with a given abstract polytope. Moreover a bijectional mapping of an abstract polytope with anaploid pieces is no longer a graph. Since the association of abstract structures and graphs with specific manifolds is a fundamental assumption of topological analysis, the modern abstract formulation opens an equally fundamental divide between the historically closely-intertwined areas of polytopes on the one hand and topology and graph theory on the other.

One might therefore be tempted to restrict one's attention to proper decompositions and cast one's definitions accordingly, as Stewart did (and indeed I did until Branko pulled me up). But in that case, one would be rejecting many otherwise valid abstract polytopes. That might not matter if an easy way were found to classify abstract forms as proper vs. anaploid decompositions, but such a method has proved deeply elusive and, to date, a failure of one of the higher aspirations of the abstract theorists. Moreover it would still leave anomalies such as the cornoid properties unexplained.

It also seems inconsistent, or at least overly restrictive, to allow a toroid as an interior but not as a building-block. One could hardly be laying claim to a general theory. The abstract acceptance of anaploid cells presents a model which is too powerful and elegant to ignore. They arise so naturally within the elegant defining properties of abstract polytopes, and are so elusive in their ability to be readily identified by any abstract properties, that they have become accepted by the abstract community as valid polytopes. And if we accept anaploid cells in higher dimensions then, for consistency, we may not reject non-disc polygons. There remains no reason to deny the Möbius pentagon vertex figure as a polygon in its own right.

However the abstract formulation captures only the combinatorics of a piece's boundary and not the topology of its body. There is thus no way for it to yield the information which it has made necessary.

The only way to provide a complete description is to explicitly define the internal topology of each and every individual piece, there is no getting away from it. From the abstract point of view, this information can only be provided at the realization stage. Topologically, one would have to declare that the polytope was an incomplete decomposition, and to further decompose each anaploid cell to determine its interior topology (and even there, in higher dimensions some abstruse 4-manifolds might trip you up). Morphic theory meets this requirement by adding it in the interpretation step of realization. The choice of manifold is arbitrary, provided it can be bounded by the incident pieces. Until this is done, the second stage of realization, into a geometric space, cannot proceed. Equally, once this choice is made, the associated manifold is now fully defined for topological purposes.

The morphic polytope thus arises as the intermediate stage created by the breaking of realization into distinct interpretative and concretizing steps. The topological approach, or at least an extension of it, turns out to be essential to both the morphic understanding and the process of realization. The individual defining of interiors, as required by morphic theory, thus lies at the heart of the reconciliation between the topological and abstract approaches.

Duality

The duality of polyhedra - the exchange of vertices with faces - has been remarked on since ancient times.

Euler's discoveries led in turn to the equivalent duality of graphs. Topologically, the dual of a polytope came to be understood as the dual graph embedded in the same associated manifold.

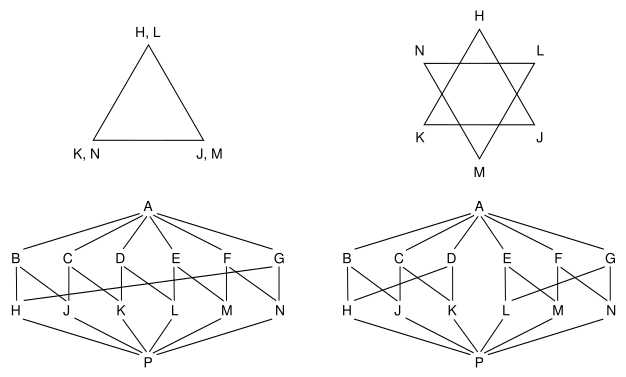
In abstract polytope theory their duality manifests in a particularly elegant way. To obtain the dual of a polytope we need only turn its Hasse diagram upside down so that the direction of the ranking order is reversed. Alternatively, you can think of it as reversing the order of ranking in the diagram, without changing it in any other way.

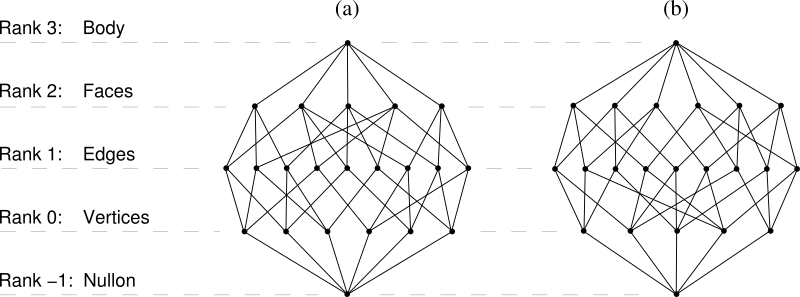
The directed Hasse diagrams of; (a) the triangular prism, (b) its dual trigonal
dipyramid. The diagrams are isomorphic but ranked in opposite directions.

This ease with which an abstract polytope may be dualised leads to a further abstraction in which the ranking sequence is defined but not its direction. The ranking direction, defining which element is minimal and which maximal and so on in between, then becomes part of the interpretation step in realization. In fact, it is a natural part of the step in which the pieces of each dimension are ordered by rank. In this picture, a polytope and its dual are two realizations of the same abstract polytope.

In the context of theoretical physics, such underlying forms common to a dual pair of entities (i.e. of equations) have recently been discussed and dubbed schemas. The principle is attractive. In this view, an abstract polytope might be more aptly named a polytope schema. As with tidiness, before I encountered abstractions or physicists I was developing much the same notion in the context of stellation and facetting, where I came to refer to schema as precursors.

Returning to the topological view, what if the polytope has anaploid pieces and is not a graph? Consider for example a star pentagonal prism with a Möbius pentagon at each end. It is topologically a Klein bottle but its graph is planar. The dual graph is the pentagonal dipyramid but it must still be embedded in a Klein bottle. Can the twist inherent in each Möbius pentagon be conserved within the dual vertex? I see no reason why not; one might well expect the twist to be evident, perhaps even defined, in the vertex figure. This will then also be a hollow Möbius pentagon and the core region of the dipyramid's interior will be hollow.

Morphic twists

The cuploid and cornoid have one more puzzle for us. In this case it is a solid, star pentagon which reciprocate to a hollow star vertex figure. How can this happen? Why does this particular dual fugure not conserve the inherent local orientability of the Cayley star? The reason lies in various complexities which I am only beginning to unravel. One set of issues revolve around anomalies in the theoretical pasis for polyhedral reciprocity, but that is another subject altogether. Another arises when an anaploid piece gets twisted around in complicated ways; the Möbius pentagon is probably the most basic example (which is one reason I chose it as a discussion point).

Given our new morphic understanding, it is now permissible for the cuploid base itself to be a Möbius band. The polyhedron is now a Klein bottle. Its dual is visually the same cornoid as before, however its apex is now open in the sense that it does not connect across from one side to the other. Both the base and its dual vertex figure are the same kind of star pentagon. Morphic theory thus offers a fully consistent solution.

But wait a minute. Are we to deny that the Cayley-based cuploid is a polyhedron because of this? It is also a permissible graph drawn, in this case, on the projective plane. There is no reason why an anomalous correspondence between face and vertex figure shoulkd invalidate it. The morphic analysis makes it clear that there must be more than one solution to the dilemma.

But as yet I have not developed the theory enough to explain the observed anomaly. Imagine fixing a loop of string around a rubber sheet. Now make the piece of string into a cat's cradle and flatten the whole thing down into the plane. What shape does the rubber take up? How does a Möbius band differ from a disc? This exercise gives a flavour for issues raised by complicated twisting up of a manifold, be it a simple or anaploid. I have made some progess in classifying the various twists and turns for polygons, but still have some way to go. Their relationship to projective polarity and reciprocity, which is the basis for constructing a geometric dual, may also need some clarification. Morphic theory at leasts provides a rational theoretical foundation for these investigations.

Regular morphic polytopes

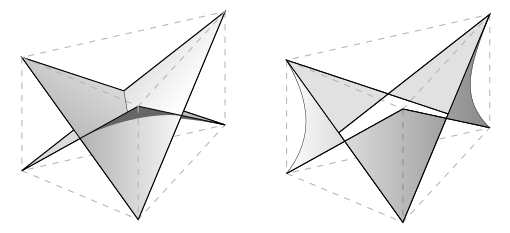
Two skew {6/2} with bodies which are respectively a
double-wound disc and a Möbius band

I confess to have broken with tradition and gone backwards. Historically, writers have tended to be be motivated by the symmetries of regular polytopes to study them first and then to generalise to the irregular as something of an afterthought. As a result their writings have often been burdened with preconceptions arising from the undeniable power and beauty of symmetries. My ideas on morphic theory have gone the other way, perhaps fortunately so for I have not been similarly burdened. Remarkably, this has led me not only to the discovery of a whole new class of geometric polytopes with anaploid pieces, but also to the presence among them of multiple new families of regular ones.

The sharp-eyed among you will have recognised that the Möbius star pentagon discussed above is not only regular but represents just such a new class of regular star polygons and, by extension, of regular star polytopes in general.

A given manifold may be decomposed and twisted up in many ways to produce distinct regular star polytopes. Similarly, any regular skeleton of a star polytope may be fleshed out by many different manifolds to yield many distinct regular stars (i.e. the associated manifold is not unique). For example a regular star hexagon {6/2} can be realized in three dimensions as a circuit of diagonals around a uniform triangular prism. By now, I hope it is not obvious to you how this skew polygon should be filled-in with an interior. Two topologically and hence also morphically distinct examples are illustrated.

As an example among the polyhedra, in an analogous situation to the Möbius star pentagon we may consider an alternative 3-manifold for the body of a small stellated dodecahedron. Besides Cayley's filling of both the interior dodecaedron and the outer pyramids, a manifold may be found which fills only the pyramids and leaves the central region hollow. Clearly, many solutions arise for each of the other regular stars, as they have many more interior layers.

In an analogous situation to the double-wound hexagon which looks like a triangle, we might alternativey consider a double-covered polyhedron which looks like a tetrahedron. The illustration below shows such a figure, the regular polyhedron {3, 6/2}. Upper left is a vertex figure, which is a {6/2} and has been pulled slightly apart to show its double-winding. {3, 6} is a regular tiling of the torus – or more precisely a family of regular tilings, since the number of repeat units may vary. To the right is the graph of {3, 6/2} as such a toroidal polyhedron, with the fundamental polygon of the toroid shown dashed. Below are two possible fillings depending on the topology of the polyhedral body; left is a conventional torus, right is a non-orientable torus or Klein bottle, which is the three-dimensional equivalent of a Möbius band.

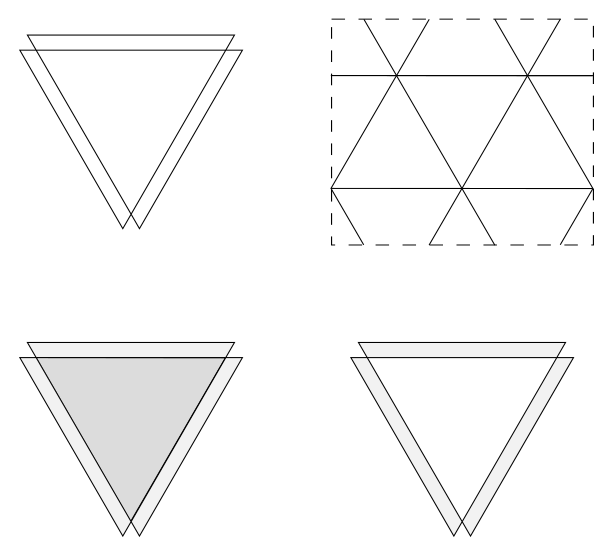
Regular polyhedra {3, 6/2}

Compounds, regular or otherwise

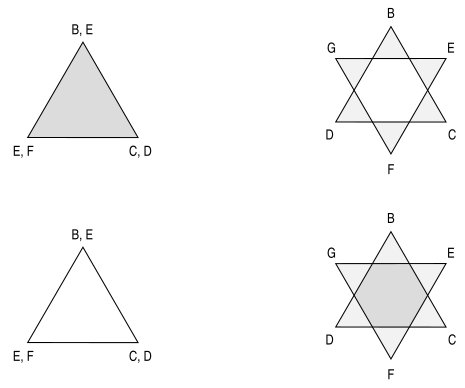
A suggestion I end with here is that the morphic approach allows a novel treatment of polyhedral compounds. For example the Schläfli symbol {6/2} is sometimes taken to denote a double-wound triangle (left hand illustrations). This concrete realization preserves the hexagonal abstract structure seen in its Hasse diagram but its geometry does not reflect that. The symbol is therefore more often taken to denote a regular compound of two triangles, the hexagram (upper right). But, while this concretizes the desired geometric symmetry, abstractly it breaks up the hexagonal structure into two triangles, thus changing its abstract symmetry.

If we instead treat the compound figure topologically and hence abstractly as a single 2-manifold with a boundary of two disconnected pieces, we may then regard any regular star polygon as a single abstract figure, as in the Hasse diagram shown (lower right), with the number of boundaries denoted by the highest common factor between the numerator and denominator of its Schläfli symbol. The abstract structure is no longer properly connected and so, although it retains its status as a single structural unit, such a polytope compound is still not a polytope and represents a slightly more general class of incidence complex. However which of the figures shown represents {6/2} must still depend on whether we interpret the symbol to reflect its abstract or concrete symmetry.

{6/2} as (left) a double-wound triangle and (right) a manifold with two triangular boundaries

One might perhaps distinguish between a "polygonal compound" such as two overlapping but independent triangles on the one hand, and a "compound polygon" such as a manifold with two triangular boundaries on the other.

Like ordinary polygons, morphic theory allows different manifolds to form the body of a compound polygon. The illustration below shows two variants for each boundary of {6/2}. Upper left is a Cayley filling of the double-wound hexagon, with below it a Möbius filling which had degenerated to zero area. On the right are two triangular cylinders, each open at both ends; above given a 60 deg turn at one end and flattened straight down, below given a full half-turn before flattening.

Example fillings of the two interpretations of {6/2}

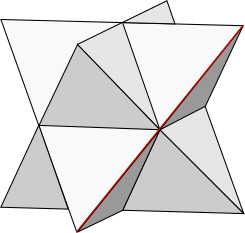
The stella octangula

The same principle of a single topological body may be applied to compounds of the regular polyhedra, especially when created as stellations or facettings of some other regular polyhedron. The stella octangula, or regular compound of two tetrahedra, is the only polyhedral compound which is truly regular, in that its flags lie in a single orbit under the symmetries of the compound (the flags of every other conventional "regular" compound lie in at least two orbits). As a single manifold with two boudaries it is therefore the only truly regular compound polyhedron. Or, should we understand there to be two regular compound polyhedra, one a stella octangula with the central octahedron filled and the other the same outer figure but with a hollow centre? Either way, can we identify a suitable Schläfli symbol for it? It does not share the same ambiguity as {6/2}; it is clearly not a {3, 6/2}. In the context of its symmetries we may treat it as a decomposed octahedron, {(3, 4)/2}. Perhaps the regular compound of two triangles might also better be wrtitten as a decomposed hexagon {(6)/2}, to distinguish it from the double-wound {6/2}.

Together the properly-connected and compound polytopes represent a slightly broader class of incidence complex and associated manifold, each having their own symmetries (they remain a sub-class of CW complexes). I suggest referring to this class as polytopal manifolds, or polyfolds. There is no need to confine such phenomena to the regular examples, however their application may be limited. For example if you reciprocate (dualise) a pair of intersecting polyhedral surfaces about a centre outside them both, there is no gaurantee that the duals will still intersect. One body making discrete appearances does occur in certain branches of higher mathematics, but it is certainly not the norm and so their treatment as a single compound polyhedron and/or polyfold is likely to be unhelpful.

Conclusion

What one chooses to call a polytope is ultimately a matter of arbitrary choice. To antiquity they were convex solids. The concept was progressively extended to include stars, surfaces, tilings (apeirotopes), point sets and ultimately wholly abstract sets. Today, convex regions of mathematical spaces lie at the heart of disciplines as diverse as linear programming and quantum probabilities. Along the way, an equally diverse range of extensions have led off in many different directions.

Some of these extensions have caught us by surprise, appearing as corollaries to others, the abstract acceptance of anaploid pieces being a case in point.

But we still baulk at other extensions. There was, for a century or so, a universal accord that a real polytope has (or is) a single, unbounded surface, its faces are topological discs, and its interior body is a trivial matter.

Abstract theory breaks this accord, inextricably endorsing anaploid pieces in higher polytopes. Morphic theory merely generalises this concept to hitherto taboo regions – both down to the plane and up to the body – and explores further corollaries of all this. Although only touched on here, it offers insight and understanding to many more thorny issues than those discussed.

But does it go too far, or perhaps not far enough? Might abstract theory be deemed to be about a wider class of object, with "polytopes" reserved for CW complexes which are also topological manifolds? Might it be useful to bring compound polytopes too under its umbrella, allowing a polytope to have a disjoint surface comprising multiple unbounded regions? Complex polytopes, in the original sense of being non-dyadic, never caught on in real space and one must question the extension of the term to complex spaces where bounded line segments and plane regions do not exist. Or will the morphic model be accepted with modification in some disciplines but not others, creating a new generation of conflicting definitions to supplant the old? Only time will tell.

References

  1. Abrams, L. and Elkind, L.D.C. (2019) "Word Choice in Mathematical Practice: a Case Study in Polyhedra", Synthese, Vol. 198, pp. 3413–3441.
  2. Cayley, A, (1859a) "On Poinsot's Four New Regular Solids", Philosophical Magazine, Vol. 17, 123-128.
  3. Cayley, A, (1859b) "Second Note On Poinsot's Four New Regular Polyhedra", Philosophical Magazine, Vol. 17, 209-210.
  4. Grünbaum, B. (2006) "Graphs of Polyhedra, Polyhedra as Graphs", Discrete Mathematics, No. 307, 2007, 445‑463.
  5. Inchbald, G. (2020) "Morphic Polytopes and Symmetries", special edition, Symmetrion. (forthcoming)
  6. Johnson, N.W.; (2018) Geometries and Transformations, Cambridge University Press. (See especially Chs 11 to 13).
  7. McMullen, P. and Schulte, E. (2002) Abstract Regular Polytopes, Cambridge University Press.
  8. Stewart, B. (1964) Adventures Among the Toroids, 2nd edn, Stewart. (1st edn 1952).