A Critique of Abstract Polytopes
Updated 13 July 2022
Abstract theory is a set-based formalism which decouples the hierarchical structure of a polytope from its geometrical form. It has proved a powerful and useful tool, even revising our ideas of what is and is not a polytope. However its origin in combinatorics has left a legacy of confusions in both its conceptual basis and its terminology, for which associated modifications are put forward here.
Contents
- Basis for abstract polytopes
- Pieces and subtopes
- The body and the nullity
- Non-simple (anaploid) pieces
- Duality
- Realisation
- Bibliography
Basis for abstract polytopes
Introduction
A polytope is the generalization, in any number of dimensions, of a polygon in two dimensions and a polyhedron in three. Just as a polyhedron can be constructed by assembling together suitable polygons, so a higher polytope may be constructed by assembling together suitable polytopes of one lower dimension.
Even the humble vertex point may be regarded as a 0-dimensional polytope, a monon. A line segment is constructed by joining two such vertex points to form a 1-polytope or ditelon (Johnson 2018 contracts it to "dion", which I find less descriptive than "polygon" or "polyhedron"; two what?)
This structural form of a polytope is in some ways more fundamental than its exact geometric appearance. For example a cube, a cuboid and a parallelepiped may have different dimensions and angles but they all share the same structural form of three quadrilaterals joined together around each vertex. An abstract polytope captures this structural form in a way which allows an algebraic approach to its study.
The algebra used is that of set theory. The language or terminology adopted is however an unsatisfactory hodge-podge inherited from different disciplines and remains in an unhappy state of change.
Informally then, in the jargon of set theory, an abstract polytope is a set of ranked members or elements, partially ordered via a ranking function and with a pairwise relation which may hold between given elements of adjacent rank.
A common way of depicting the ranked and pairwise related structure is its Hasse diagram, named after number theorist Helmut Hasse. Here is the Hasse diagram of the abstract cube.

Hasse diagram of the abstract cube.
The diagram shows the ranked elements as dots and their pairwise relations as lines. The main ranks correspond to the individual elements of the geometric figure - vertices, edges, faces, etc. and are numbered to correspond with their number of dimensions. The abstract cube has five ranks, even though the geometrical cube has only three dimensions. This is because a rigorous algebraic theory is made far simpler by adding a "maximal element" and a "minimal element" to the set. For a polytope in n dimensions, an n-polytope, the maximal element has rank = n. The minimal element is ranked lower than the 0-dimensional vertices and so is given rank = −1. An n-polytope thus has ranks = j for −1 ≤ j ≤ n. The pairwise relation is called "incidence".
A less graphical depiction is the tabular incidence matrix. These require labelling but can be easier to interpret for more complicated polytopes. They are not necessary here.
The set-theoretic definition imposes certain structural properties which Johnson has summarised as monal, dyadic and properly connected.[6] These conditions essentially bar monsters such as repetition of the same element, configurations, objects joined at a single vertex, compounds, and so on. However, as shall be seen, some unanticipated monsters can still slip past the bars (Monster-barring is an acknowledged procedure whereby the mathematician binds their definitions up in additional elaborations to try and prevent unwanted consequences of their theory).
The simplest valid abstract polytope is the 1-polytope or ditelon. Below that, the 0-polytope or monon corresponds to a point, while the −1-polytope or nullon is a null polytope analogous to the empty set ∅ or the number 0. These two sets are too simple to be dyadic and so are not, strictly, abstract polytopes. However it can sometimes be convenient to treat them as such.

Labelled Hasse diagrams respectively of the nullon, monon, ditelon and digon.
Origins
Through the twentieth century, inspired in part by the study of discrete geometries comprising sets of points, theorists developed a view of convex polytopes as sets of vertices, i.e. as lattices. An edge was just a vertex pair, a polygon a cyclic set of such point pairs, a polyhedron a partially-ordered set of such cyclic sets, and so on. Everything was described in terms of combinations of vertex points. It was a short conceptual step to generalizing the notion for all polytopes, not just the convex variety; however the theory proved less easy to generalise.
Meanwhile topology relied on the decomposition of a surface into polygons (or a hypersurface into polytopes) in order to study its overall form. This gave rise to the idea of incidence complexes as sets of geometric elements such as points, line segments, plane regions and so on. An n-polytope (a polytope immersed in some n-space) was just such a decomposition of some unbounded (n−1)-manifold or (n−1)-space. The decompositions equivalent to polytopes became known as CW complexes. Significantly, such polytopes need not be convex.
The stage was now set for a merging of the two approaches. Abstract polytope theory took shape slowly, much along the lines of convex polytope theory but with the demand for convexity abandoned.
Around the turn of the millennium various problems with this approach began to emerge. Johnson in particular championed certain clarifications, based on his own interpretation of Euclidean space as a set of points, with every j-dimensional element of a polytope therefore being a subset or region of some j-dimensional subspace. Discussion of these and other such problems forms the bulk of this essay, along with suggestions towards their resolution.
Terminology
Although this introduction has stuck mainly to the language of traditional set theory, abstract polytope theory has its own distinct vocabulary. Unfortunately, it is more accurate to say that several distinct and incompatible vocabularies have grown up over the years. Its terminology has caused, and is still causing, great problems. Both topological and combinatorial treatments adopted terms from traditional polyhedron and polytope theory, though they did so piecemeal and with little consistency. As the abstract programme attempted to establish a common ground between the two theories, it did so in the context of all those original polytopes. Thus it found itself with three incompatible vocabularies which needed to be reconciled. One way forward was to coin its own terms or change the usage of established ones, which of course led to a total of four incompatible vocabularies. Over the last half-century various writers have chipped in with their takes, Johnson included. Established writers periodically updated their own vocabularies as they lost patience with particular inconsistencies. There are now probably more dialects than there are authors. The process continues in 2020 with, for example, McMullen wisely abandoning "facet" and "section".
Duality was never a primary issue. However the case I present here puts it right at the heart of the abstract formalism, a state of affairs which arises directly from my investigations into what I call precursors to dual pairs and finds an intriguing parallel in modern theoretical physics.
So now we have a fifth vocabulary raising its game and demanding to be made intelligible. I believe that the most useful way forward is to forget the chaotic heritage and go back to traditional polytope theory as a starting point. Where a particular abstract-related concept emerges, one may then adopt whatever term seems most intuitively understandable within that context, while as far as possible avoiding unnecessary inconsistencies with other disciplines. I therefore make no apology for cutting a fair old swathe through the historical mess and introducing a sixth vocabulary, nor for revising it from time to time as I see fit.
Pieces and subtopes
I will say that the members or elements of an abstract polytope are its pieces. A piece of rank j is a j-piece and has, or is of, dimension j. "Faces" has risen to common use so I need to give some account of my change to "pieces". First, "faces" as a generic term causes the novice some confusion with the traditional polygonal faces of polyhedra. Secondly, as discussed below, there has been endless confusion as to whether or not a face should include its boundary, and cutting the knot clean away seems a safer approach than picking sides. "Piece" has long been used in topology, where the issue of boundaries is well worked out, and can be adopted in the abstract realm with no loss of consistency.
Within an abstract polytope one may find embedded other abstract polytopes with fewer ranks, i.e. of lower dimension. For example the above Hasse diagram of digon ⟨A; B,C; D,E; F⟩ includes ditela such as ⟨A; B,C; D⟩ and ⟨B; C,D; E⟩, monons such as ⟨A; B⟩ and, trivially, nullons such as ⟨A⟩ and ⟨D⟩. These are its sub-polytopes or subtopes. (Note the use of chevron braces ⟨⟩ to denote a set which is a polytope.)
The boundary of a polytope is the set of incident j-pieces for j = 0 to n−1. That is to say, it lacks the maximal and minimal elements and so is not itself a polytope. The boundary of the digon is the set {B,C; D,E}. The boundary of ditelon ⟨A; B,C; D⟩ is {B,C}.
We now face a curiously contentious issue. Is an edge of the digon better defined as some piece such as D, as its boundary {B,C}, or as the subtope ⟨A; B,C; D⟩? The topologists generally went for D, the combinatorialists for {B,C} such that D is a convenience more fully defined as {B,C}. Moreover a circuit of vertex pairs such as triangle {AB,BC,CA} was clearly a "face" and therefore so was the triangle element, say F.
Johnson in particular helped to persuade the combinatorialists that actually it was the other way round, with D being the edge and equating it with {B,C} was their convenient interpretation. But you will still find texts fighting a gallant rearguard action. Despite all this the third alternative, of treating an edge as a subpolytope, a ditelon, remains a popular understanding.
Certainly, when you look at the ranked diagram is is absurd to suggest that the pieces do not represent vertices, edges, faces and so on. It is perfectly valid to say that the polytope is constructed from them all. But what of the popular conception that it is constructed from subtopes? One may note that such a construction procedure requires the joining of adjacent subtopes such that pieces of their boundaries merge. This revised process is as valid as that using the bare pieces. In other words, both views are correct, as long as you specify the appropriate construction procedure.
With this sorted out, it is time to define some more terms.
Some pieces of specific dimensionality have specific names:
- Nullity: the −1-piece or null piece.
- Vertex: a 0-piece.
- Edge: a 1-piece.
- Face: a 2-piece.
- ...
- j-piece: a piece of rank j. Piece F of rank j is denoted by Fj.
- ...
- Cell: an (n−1)-piece of an n-dimensional polytope; an edge of a polygon, a face of a polyhedron, etc.
- Body: the n-piece or maximal piece.
Subtopes are often called "sections", a source of constant confusion with the sections in descriptive geometry which are familiar to every student of technical drawing. McMullen has recently given up on it and changed to "subposet". However, since an abstract polytope itself is a particular kind of poset (short for partially-ordered set) and other kinds of (sub)poset are also embedded in it, "subtope" better echoes the poset's nature as specifically a polytope.
If an unbroken downward chain of incidences runs from some face F to another one G, they are said to be connected and we write G ≤ F. In some vocabularies the incidence relation is instead treated as transitive and we may say that F and G are incident, for example that a face of a cube is incident with four vertices.
A subtope comprises the set of connected pieces between its maximal element F and minimal element G and is written F/G. Some types of subtope are important enough to have their own names:
- Span: of a piece F is the subtope F/F−1.
- Cospan: of a piece F is the subtope Fn/F.
- Cell span; the polytope corresponding to a given cell. For example a face span is a polygon. (Often conflated with the cell itself).
- Vertex cospan: may be realised as a vertex star or a vertex figure.
We may now conveniently interpret a vertex as a point, an edge as a line segment, a face as a plane region and so on. If we interpret them as open, i.e. excluding their boundaries, then their spans are the same extents but bounded. Abstractly, this seems to be the best combination of clarity and rigour yet devised.
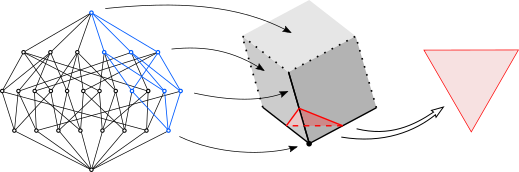
Vertex cospan (blue), vertex star and vertex figure (red) of the cube.
The body and the nullity
Polyhedra were originally "solids". As Poincaré vastly advanced topology a little over a century ago, he included bounded as well as unbounded manifolds. Just as the surface of a polyhedron was an unbounded 2-manifold, so its body was a bounded 3-manifold. Both could be analysed as CW complexes. However, since the bounding surface is already a CW complex, while the body must be temporarily subdivided into cells for topological analysis, the emphasis soon shifted to the surface. This was further reinforced by the combinatorialists, who had no interest in the body. Throughout the twentieth century, most definitions of a polyhedron came to describe it as a surface. (Not that this stopped such people propmptly talking of say the "regular solids" as they had always done.)
Yet abstractly, every n-polytope has a maximal piece or body of rank n and a minimal piece or nullity of rank −1. While all the other pieces represent tangible elements of the geometric surface and are described as "proper", these two were originally added only for the sake of set-theoretic convenience. Adding them cleaned up the set-theoretic formulation most elegantly. The body was just the "master set", the polytope itself, while the nullity was deemed to be the empty set. But, because they did not appear to represent any part of the surface complex (which was all that anybody remembered any more), they were thought of as "improper" pieces, and often still are.
The issue is often further confused by the fact that every set contains as subsets both itself and the empty set, so at first sight it seems natural to include them in the formulation. However there is a fundamental and highly significant distinction between inclusion as an element and mere containment as a subset. There are many other subsets which the polytope contains but we do not include as members, such as the ranks or the cospans, so why pick out just two of them? In is an improper thing to do, which is perhaps how they picked up that particular epithet.
Now, when we move the abstract formulation beyond combinatorics and generalise the pieces to mere placeholders, the polytope becomes a set of primitive elements and any rationale for its definition as a set of sets collapses. The rationale for regarding the maximal and minimal pieces as improper collapses along with it, while they remain necessary ingredients of the theory.
There is another reason why the maximal element is not improper. Let us at last remember the two thousand years of tradition, in which nobody ever talked of the "Platonic surfaces". The interior of a polytope has come to be called its body. Once we accept the body as a valid part of a polytope, or at least a valid interpretation, then its place as the n-dimensional piece becomes obvious. Its span is the polytope itself. There is nothing improper at all about that.
The minimal element has no such intuitive interpretation. Nevertheless it remains a valuable construct of the set-theoretic model. We may interpret it as a geometric null, not even a zero-dimensional point, hence Johnson named it the nullity. It is not even a null polytope; that privilege goes to the set of which the nullity is the only piece. But it is not wholly insignificant, for example its cospan is the whole polytope.
Consider the vertex cospan of the cube, illustrated earlier. Once extracted from the cube as a vertex star, the core vertex point of the star is, abstractly, its minimal element. So even though a lack of geometric existence sometimes makes it seem improper, that is not always the case and of course any impropriety is just a particular geometric interpretation; the abstract expression has none such.
There is one more common abstract fallacy to expose. Many abstract theorists still insist that the nullity, the null polytope and the empty set are all one and the same. Yet if the nullity were the empty set, then somehow when the vertex star were extracted its minimal element must not merely lose a rank but suddenly become the empty set, surely an awkward and mathematically unjustifiable impropriety in its own right. Indeed, the only abstract impropriety in the whole exercise was to regard the nullity as necessarily being the empty set.
Non-simple (anaploid) pieces
Schulte notes that; "In some sense [the dyadic] condition says that P is topologically real. Note that the condition is violated for nonreal complex polytopes." In other words the diamond or dyadic property of an abstract polytope implies a structure in real space, as the property is violated by complex polytopes.
His remark arises because the dyadic property is also a necessary consequence of the proper decomposition of a manifold, be it given a real or Riemannian (complex) metric. It illustrates the profound distinction between a manifold and a configuration, reaching down to the topological properties of the object and quite independent of the metric subsequently applied to its form. It thus lends support to the notion of a real polytope as a piecewise manifold, as distinct from a real configuration.
If the nature of a polytope as having a real surface is to be respected then the body of every j-piece must be realised as a real region. In its topological analysis this leads to the requirement that every such j-region be homeomorphic to a j-ball. In plain language this means that an edge must be a single line segment, a face a contiguous plane region like a disc, a cell a smooth solid region like a ball. For example it must be possible to cut a face out of a piece of paper without any joins so something like a Möbius strip, which has a twist in it so that it must be cut and joined, is not allowed. In topological speak, such a cell or ball is a j-ball, a face or disc is a 2-ball and a line segment is a 1-ball. Such balls are said to be simple. Many polytopes, such as toroids and the uniform hemi polyhedra, have surfaces which are not simple; toroids form holes, hemi polyhedra form twists. Consequently their bodies cannot be simple either, indeed it is often not clear what the topology of any body might be. Thus, in topology it is not possible to use just any kind of polytope to construct a higher one, you have to restrict yourself to those which have simple bodies and simple subtopes, all the way down to their edges, in other words to CW complexes.
However the abstract definition allows such non-simple pieces. I shal call such topologically non-simple objects anaploid from the classical Greek απλους (aplois) meaning simple. For such polytopes, it is often not clear what the topology of the polytope surface might be. One approach is just to abandon any idea of realising the body, but then it is no longer possible to treat the polytope as a manifold and the justification for insisting that it be dyadic is lost.
Abstract polytopes incorporating anaploid pieces such as projective planes or toroids have no counterparts in any traditional definitions of a polytope. Since they are no longer CW complexes, basic tools such as Euler's formula and its higher-dimensional derivatives no longer yield useful topological information about them. One might have hoped that combining the definitions of an abstract polytope and a CW complex would be easy enough and the abstract definition could then be modified accordingly. Indeed, such a goal seems to have been one of the original motivations for abstract theory. But it has turned out to be an exceedingly tough problem, with the non-CW monsters roaming free and unbarred. This entrenched difficulty is suggestive that no simple, elegant solution may exist.
Yet these particular monsters arise so naturally from the elegant defining properties of abstract polytopes, and are so elusive in their ability to be readily identified from any abstract properties, that they have become accepted by the abstract community as valid polytopes, developing a strong theoretical base on their own terms. To draw in another metaphor, the genie is out of the bottle.
Duality
Since the days of Euler, a polyhedron has been understood as a graph drawn on the associated surface manifoled. Grünbaum has pointed out that a simple extension to graph theory to higher dimensions allows us to understand any polytope as a (higher-dimensional) graph drawn on the associated manifold. The dual polyhedron or general polytope may be easily constructed, merely by drawing the dual graph on the same manifold.
The dual of an abstract polytope is obtained in an even simpler, one might say beautifully simple, way; by reversing the order of ranking. That is all. Ranks n and −1 exchange numberings, as do ranks n−1 and 0, and so on. The incidence relations remain unaffected. One can think of it as just turning the Hasse diagram upside down.
However the combinatorial set-of-vertex-sets formulation raises a serious problem. The various subsets can not simply be re-ranked, as the cells have now become vertices and vice versa. The old subsets have to be discarded, the new vertices relabelled and new subsets recreated, typically with different combinatorial structures from the old.
Another problem with that formulation is that the piece identified with the empty set gains rank n. Yet according to the set-of-sets formulation the empty set must have rank −1. Since the defining properties of an abstract polytope do not allow an element to occur twice, it is impossible for the new piece of rank −1 (formerly the body) to also be the empty set. The dual is no longer a valid abstract polytope.
This last can of course be fixed in the general reorganising of the subsets, a procedure typically regarded as of trivial significance. However while it may be conceptually trivial, it is messy and time-consuming; it breaks the beautiful simplicity of reversing the ranking order, oveturning the Hasse disgram, or drawing the dual graph on the associated manifold. It strongly suggests an approach of treating the subsets, and especially the empty set, as a combinatorial convenience or interpretation rather than a definitive property.
Realisation
The abstract description deliberately says nothing about the geometric appearance of a polytope. In order to relate structure to geometry the notion of a geometric realisation had to be introduced.
Realisation refers to the process of deriving a geometric figure from its corresponding abstract representation. The abstract form is said to be mapped or injected into some containing space, usually Euclidean. Any given mapping of any given abstraction into any given space will result in a particular geometric figure, and for every geometric polytope there will exist such a mapping.
Abstract theory is deliberately somewhat woolly about the details of this process. The idea is that you can choose your mapping rules to suit your interest. For example if it lies in convex polytopes then you will want the mapping to be a bijection with the union of certain half-spaces, if in regular polytopes then it must map the abstract symmetries to their geometric counterparts, if in polyhedra with hollow faces then you may choose not to realise the 2-pieces at all, or to map them onto their geometrical boundaries, and so on.
Realisation of the nullity can also be a haphazard affair. When a polytope is realised in some space, much of that space remains external to the polytope, it is as it were a no-polytope region. Thus, it may sometimes be useful to map the nullity to the exterior region, for example when the geometric figure surrounds cavities which are exterior to the manifold but nevertheless enclosed by it. In this sense the abstract figure maps to the whole of the destination space, since the nullity is mapped to all regions from which the other pieces are absent.
Nevertheless, the abstract theorists have not been able to resist imposing some of their own, broader preconceptions on the process.
Faithfulness
Many possible mappings will result in figures which do not have the traditional attributes of a geometric polytope and which we conventionally regard as degenerate or improper. Faces might be curved, pieces superimposed or intersecting, the whole thing may be flattened into fewer dimensions or skewed into more, and so on.
At this point the theorists felt compelled to indulge in a little more monster-barring, elaborating on various requirements under the banner of "faithfulness". A geometric figure is said to be a faithful realisation of an abstract polytope if it meets the various criteria laid down.
Thus one must decide whether the mapping must be bijective or whether pieces may be mapped one-to-many and/or many-to-one, whether all pieces must necessarily be mapped at all, whether each piece must be mapped into its own flat subspace, and so on.
However the great variety of mathematical interests, which led to the abstraction of structure from geometry in the first place, are mirrored in an equally great variety of ideas as to what figures should or should not be regarded as faithful. For example when we consider the metamorphoses of polygons, should we suddenly declare the figure unfaithful every time one part momentarily passes over another? Is self-intersection permissible, as with the regular star polytopes? What about spherical polytopes and their curved pieces?
The one thing we must not do, at least not without a lot of careful investigation first, is to make any of these variations a formal abstract entity and imagine we are still discussing the same theory. For our results may well not transfer sensibly to other approaches. This mistake can be seen as a common thread across a great many of the historical anomalies and arguments between rival theories of polyhedra.
Realisation thus resolved little, becoming in effect a woolly rag-bag into which all those habitual problems, old and new, have been thrown. The attempt to invoke faithfulness merely kicked all those problems further along still. It seems that in order to avoid an infinite regress of monster-barring games, a rather different approach is needed.
Apeirotopes and bodies
Abstractly, an infinite polytopes or apeirotope is just an infinite set which meets the definition of an abstract polytope. Typically an apeirotope of dimension n may be realised as a tiling or honeycomb entirely filling its own n-space. Some may be realised as skew sponges or tiled subspaces which divide a containing n+1-space into two equal parts. Some may be realised in an n+2- or higher-dimensional space which they do not divide at all. In all these cases there is no way to identify an inside and an outside, nowhere to unambiguously map the body onto.
On the other hand it is perfectly possible to map an apeirotope onto a finite solid. For example a Poincaré disc is an infinite hyperbolic plane mapped onto a finite disc and such discs are sometimes used to depict hyperbolic tilings. Several such topological discs may be squashed into polygons and the tilings joined piece-to-piece to form an apeirotope with a finite body. The delightful spidron polyhedra of Dániel Erdély provide another example.
Should all these realisations, especially skew examples in much higher spaces, be regarded as faithful? If not, why not? Opinions differ. But that is all they are, opinions.
Johnson's real polytopes
In an attempt to iron out the worst of the problems with the set-of-sets understanding and its realisation, Norman Johnson (after whom the Johnson solids are named) developed a theory of real polytopes. He defined a real space as a locally-Euclidean set of points, typically identified by Cartesian (x, y, z, etc.) coordinates. The various pieces of an abstract polytope were then realised as appropriate open subsets of points, comprising particular regions of space without their boundaries. The boundary was provided by the incident sub-pieces. For example a face was an open region of a plane, an edge an open line segment and a vertex a point. The union of all these sets constituted the whole polytope.
This gave him the rigour to debunk the idea of identifying an abstract piece with its boundary or its span, thus forcing the combinatorialists to retreat into realisation and a non-rigorous but stubborn "convention". On the other hand the empty set admirably fitted his point-set model of the minimal piece and he was happy to maintain its identity with the nullity.
However his treatment still had problems. Most significantly, his definition of the boundary made it impossible to recognise holes within a self-intersecting realisation. For example the vertex figure at the apex of a cornoid is a star polygon with a hollow centre. Enclosed as it was by the polytope boundary, his model insisted that it must be filled. Less mortally, it deemed that a faithful realisation may have overlapping pieces if they poke inwards but not if they poke outwards, a result which sits awkwardly with the metamorphoses of polytopes. Then again, if the nullity is realised as the empty regions of space, it is clearly the largest point set of all and can in no way be identified with the empty set.
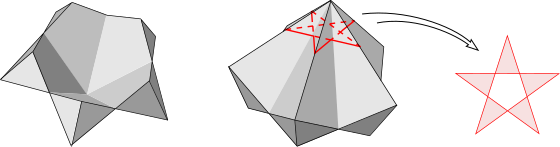
The vertex figure (red) at the apex of the pentagonal cornoid has a hollow centre.
An early version of Johnson's theory and terminology is set out and discussed in "Polytopes - Abstract and Real" and his final version is summarised in his book on Geometries and Transformations (CUP, 2018). See Chapter 11: Finite symmetry groups).
Realisation in two stages
All the above has led me to develop the present form of what I call morphic theory and the suprising discovery of many new morphic polytopes which arise from it. In the present context, morphic theory resolves the dichotomy between the abstract and topological formulations through a particular approach to realisation. Specifically, it lends itself readily to a distinction between two sequential steps or stages to the realisation process, which I call interpretation and concretisation.
The first step of interpretation defines the objects that each rank of abstract elements represents. To take a famous and somewhat apocryphal remark of Hilbert's slightly out of context, we could interpret abstract faces, edges and vertices as real tables, chairs and beer mugs without any loss of rigour. The combinatorialist interprets them as sets of point sets. However to push Hilbert's example a step further, one would have to have enjoyed the drinking party immensely before one might countenance the proposition that a chair is nothing but a pair of beer mugs, or that a table is merely a cycle of such chairs. One might observe that there are two beer mugs associated with each chair, and so many chairs set in order around the table, but defining these objects on such a basis is clearly on a par with pink elephants. None of that is adequate for the sober traditional geometer; they will want to choose such geometrical entities as points (vertices), line segments (edges), surface regions (faces) and so on, such that their dimension matches their ranking. The incidence relation may then typically be defined as a physical connectivity.
A particular consequence of the abstract predilection for anaploid pieces is that the body of any such piece must be explicitly defined in terms of its topology as a bounded manifold in its own right. Indeed, in the full morphic picture, even a simple boundary may contain an anaploid surface; for example the hollow star pentagon of the cornoid vertex figure is understood to be a simple pentagonal circuit bounding a Möbius strip. Since a given piece may thus be given different interpretations of its interior, and each such interior leads to a different polytope, the only rigorous approach is to explicitly define the interior topology of every single piece from two dimensions up (a 1-piece or line segment has only one possible topology). Yes it is horribly laborious, but if you want a rigorous approach to defining a specific anaploid geometric polytope as a specific realisation of some abstract polytope, then it is inescapable.
At this point the pieces may have a defined topology but they still have no definite size or shape. Their assemblage nevertheless comprises a topological manifold, a "rubber-sheet" figure. Specifically, it is a bounded manifold, the boundary being the polyhedral surface and the rest of the manifold its body. This contrasts with the main twentieth-century focus on the bounding surface, instead harking back to the original idea of a solid body.
The second step of concretisation is to create a specific geometric figure by injecting the manifold into some geometric space, typically one with a metric so that it gains angles, lengths, areas and volume. It is at this stage that we decide whether faces should be flat and edges straight, as a conventional polyhedron, or whether other properties such as curvature, skewing, hollowness or intersection are allowed.
The alert reader may complain that the woolly rag-bag of issues has now been kicked further along into the concretization step. That is only partly true; some of the issues were ironed out at the interpretation stage, so the morphic approach at least organises the rag-bag into two conceptual levels, thus leaving the last stage with fewer than before. In particular, the explicit "rubber-sheet" interpretation tames the monsters introduced by abstract theory. Whether this affects the criteria you care about is up to you.
Bibliography
- Burt, M.; "Polyhedral Sponge Structures: New Imagery and Inspiration for Innovative Space Structures", IASS conference, Beijing, 2006.
- Coxeter, H.S.M.; Regular Polytopes, Methuen 1948, 3rd Edn. Dover 1973.
- Erdély, D., "Spidron System: a Flexible Space-Filling Structure", Symmetry: Culture and Science, Vol. 11, Nos. 1-4, 2000. pp307-316.
- Grünbaum, B.; Convex Polytopes, Wiley 1967, 2nd Edn. Springer 2003.
- Grünbaum, B.; "Metamorphoses of Polygons", The Lighter Side of Mathematics: Proc. Eugene Strens memorial conference, ed. Guy et.al., Math Assoc America, 1994, pp.35-48.
- Grünbaum, B.; "Polyhedra with Hollow Faces", Proc. of NATO-ASI Conference: Abstract, Convex and Computational, Toronto, 1993, eds. T.Bisztriczky et al, Kluwer Academic, 1994, pp. 43-70.
- Grünbaum, B. (2006) "Graphs of Polyhedra, Polyhedra as Graphs", Discrete Mathematics, No. 307, 2007, 445‑463.
- Inchbald, G.; "Morphic Polytopes", 2020. http://www.steelpillow.com/polyhedra/morphic/morphic.html
- Johnson, N.W. (ed. Inchbald, G.); "Polytopes – Abstract and Real", steelpillow.com, 2008. http://www.steelpillow.com/polyhedra/johnson.html
- Johnson, N.W.; Geometries and Transformations, Cambridge University Press, 2018.
- McMullen, P; Geometric Regular Polytopes, CUP, 2020.
- McMullen, P. and Schulte, E.; "Regular Polytopes in Ordinary Space", Discrete and Computational Geometry, Vol. 17, 1997, pp. 449-478.
- McMullen, P. and Schulte, E.; Abstract Regular Polytopes, Cambridge University Press, 2002.
- Pearce, P.; Structure in Nature is a Strategy for Design, MIT, 1978.
- Poincaré, H.; "Analysis situs", J. Ecole Polytech. (2) 1, 1895. pp.1-121.
- Richeson, D. S.; Euler's Gem: The Polyhedron Formula and the Birth of Topology, Princeton, 2008.
- Schulte, E.; "Chapter 18: Symmetry of Polytopes and Polyhedra", in: J.E. Goodman, J. O'Rourke, and C. D. Tóth (eds), Handbook of Discrete and Computational Geometry, 3rd edn CRC/Taylor & Francis, 2017.
- van Ballegooijen, W., Gailiunas, P. and Erdély, D.; "Spidronised Space-fillers", Bridges Banff: Proc. 12th Annual Bridges Conf., 2009, Tarquin, 2009. pp.271-278.
- Wachman, A., Burt, M. and Kleinmann, M.; Infinite Polyhedra, Technion, 1974, 2nd Edn. 2005.
- Wenninger, M.; Dual Models, Cambridge University Press, 1983.