Towards Stellating the Icosahedron and Facetting the Dodecahedron
New findings on stellation, facetting and untidy polyhedra
Updated 19 Dec 2020
The text of this article is substantially reproduced by kind permission from:
Inchbald, G.; "Towards Stellating the Icosahedron and Facetting the Dodecahedron", Symmetry: culture and science Vol. 11, 1-4 (2000) pp. 269-291.
A few changes have been made. In particular, "faceting" is changed to "facetting" throughout, in line with other recent papers. Generators are renamed precursors. JCP Miller was a colleague of Coxeter, not a mentor. There are other minor corrections and clarifications.
Abstract
In describing the stellations of the regular icosahedron, the use of cell sets is inappropriate. Consideration of the rules for stellation leads to investigation of the duality of stellations and facettings. The facetting diagram of the regular dodecahedron and complete stellation diagram of the icosahedron are presented. Polyhedra which extend to infinity, have holes in, or have n-methoric or n-synaptic edges must be considered. Such untidy polyhedra are in contrast to the mathematically tidy ones more usually studied. Some illustrative examples of stellated icosahedra and faceted dodecahedra are discussed.
Contents
Introduction
The regular icosahedron is one of the five Platonic solids. Its stellations are very beautiful and were thought to have been understood over sixty years ago [1]. However there are some problems with this analysis, and I have been taking a fresh look. My first efforts [2] found some lost stellations, but failed to make sense of the whole process. This paper brings together the main areas I have worked on since then, and (I hope) moves a little closer to understanding the problem. Much of this paper originally appeared as a set of web pages – they are rewritten here with significant new material.
Stellation is the process of extending the faces of a polyhedron until they meet to form a new polyhedron. A number of references on stellation can be found elsewhere in this journal at the end of [3]. The new volumes of space enclosed by the extended faces are called cells. In the case of the icosahedron the faces can be extended repeatedly, and the cells form many layers, or shells, around the original icosahedron. Different combinations of these shells form different stellations, but not all possible combinations make acceptable stellations. The question is, which ones are acceptable?
Facetting is the reciprocal process to stellation, in which regions of a polyhedron are cut away to reveal new faces. There is a beautiful and perfectly symmetrical relationship between stellations of one polyhedron and facettings of another – in this case, the regular icosahedron and dodecahedron respectively. Much of this paper explores that symmetry and the lessons to be learned from it. Enumeration of the stellated icosahedra and the faceted dodecahedra must still wait for another day.
I must confess to one lazy habit. The stellated icosahedra are often referred to simply as icosahedra, and arguably they are because they all have 20 face planes. The faceted dodecahedra can have widely differing numbers of faces, and are not strictly dodecahedra. However for convenience I sometimes refer to them simply as dodecahedra.
Boundary Conditions for Stellation
Having failed to find an intuitively correct set of stellations for the icosahedron, I found that I was repeatedly trying to answer the question, "What are the criteria for allowing as a stellation any given collection of cells?" (We will see that this question is rather simple minded, the ruling principles have nothing to do with cells). These criteria may be thought of as boundary conditions for stellation in general, applicable to all polyhedra. I investigated a variety of conditions broadly as follows:
Miller's rules. These rules were originally proposed by a student to his colleagues [1]. They were not derived from any rigorous background theory and the students had no clear idea of their outcome. They have been followed slavishly by many other investigators for over sixty years, and are desperately in need of an overhaul. All they actually do is specify the overall symmetry, forbid any kind of internal struture, misunderstand what 'faces' are and generally mess up the issue of connectivity. I give a fuller commentary in [2].
Connectivity. The cells created by the face planes of a polyhedron typically lie in shells around the core polyhedron. A stellation should comprise a single connected set of these cells, but how connected? Face-connection means they are a contiguous solid. Edge-connection, as in many respectable polyhedra such as the 'hemi' solids, may or may not allow faces to run across connected cells, depending on whether adjacent face regions are coplanar. A corner point is called a vertex. Vertex-connection, as in a full mathematical cone, may or may not allow edges to run across connected cells, depending on whether adjacent edge segments are collinear. Which should be allowed?
Faces and internal structure. Polyhedra such as the star polyhedra and many uniform polyhedra have an intricate internal structure as their faces criss-cross inside. For some stellations the arrangement is obvious enough, for example the compound of five tetrahedra has twenty interpenetrating triangular faces. For others, the arrangement of faces, edges and vertices inside the solid is less obvious and bears careful consideration. This led me to consider the stellations' duals, because features on the inside of a polyhedron usually reciprocate to features on the outside of its dual.
Dual polyhedra. Every polyhedron has a dual, or reciprocal, polyhedron (see below). The relationship is precise and symmetrical. I realised that whatever rules hold true for stellations, exact reciprocal rules must hold true for their duals. This has proved the key in understanding the problem and has led to some interesting observations.
Duality
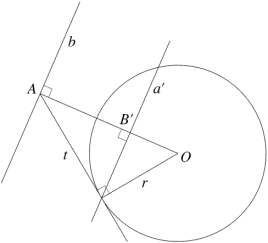
In two dimensions, according to the principle of duality any polygon has a dual, or reciprocal, polygon obtained by reciprocation with respect to a circle. Each vertex of the dual polygon corresponds to an edge of the original, and each edge corresponds to an original vertex. The relationship, shown in Fig 1, is reciprocal, which simply means that the dual of a dual is just the original polygon again.
In Fig 1, A and a' are reciprocal, as are b and B'. OA x OB' = r2. So, for r = 1, OB' = 1/OA, i.e. the lengths of OA and OB' are reciprocal. A and B' are vertices of their respective polygons. In the case of planar polygons, a' and b are edges and t is a tangent to the reciprocating circle. The same principles of construction apply whether any given vertex or edge lies inside or outside the circle.
Similarly in three dimensions, the dual of a polyhedron may be obtained by reciprocation with respect to a sphere. Each vertex of the dual corresponds to a face of the original, and each dual face corresponds to an original vertex. Fig 1 may again be used, but in the case of polyhedra the lines represent sections: a' and b through faces, the circle through the reciprocating sphere and t through the tangent cone with apex A. The dual of the icosahedron is the regular dodecahedron. Fig 2 shows them reciprocated about a sphere tangent to their edges (their common intersphere). Note that each edge has a corresponding dual edge, which is orthogonal both to the original edge and to the radius normal to both edges.
|

|
| Fig 1 Reciprocation |
Fig 2 The icosahedron (light) and dodecahedron (dark) in reciprocal relationship |
For every stellation of a polyhedron there is a dual, or reciprocal, facetting of the dual polyhedron. Likewise, for every facetting there is a reciprocal stellation. There is an exact one-to-one correspondence. By studying the duals of various stellations, we can gain significant insights into what is, or is not, an acceptable feature of a given stellation. Indeed one way to enumerate the stellations of the icosahedron would be to enumerate the facettings of the dodecahedron and then obtain their duals.
Facetting the dodecahedron
Just as the process of stellation keeps to the original face planes of a solid and adds extra edges and vertices outwards, so facetting must keep to the original vertices as it cuts away to reveal extra edges and faces inwards. No new vertices can be created, so all edges must run between vertices of the original polyhedron. Every vertex can share an edge with every other vertex. Faces may be formed wherever coplanar edges bound a polygon (note that jewellers, crystallographers, and often even polyhedron modellers, use the terms "facet" and "facetting" with rather different meanings).
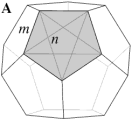
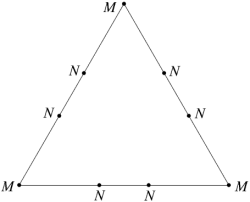
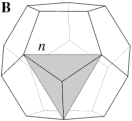
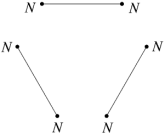
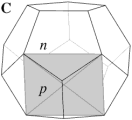
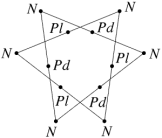
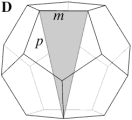
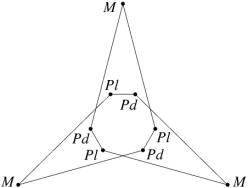
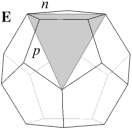
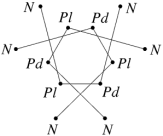
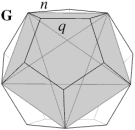
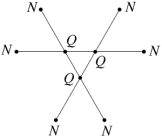
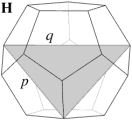
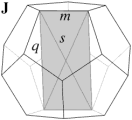
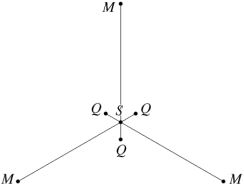
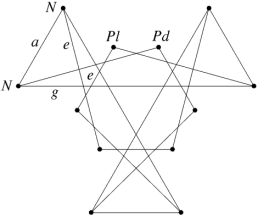
In the case of the faceted dodecahedra, the face planes fall into ten congruent sets which may be identified as A to K (omitting the symbol I). The edges also fall into five congruent sets m to q (omitting the letter o). Table 1 shows each set of face planes in two illustrations. The first shows the available edges and bounded area(s) of a face plane which can be used to form faces, located within the dodecahedron. The second shows the vertex figure for the complete set of these edges and bounded area(s). A vertex figure can be thought of as the cut surface exposed when a corner of the polyhedron is sliced off. Below these is a note of the face plane set's important features.
Note that the vertex figures show the edges and faces in section, so edges m to q appear as points M to Q. Edges p occur in distinct dextro (right-handed) and laevo (left-handed) subsets, respectively pd and pl. Where the vertex figure does not form a closed polygon, the face set does not close space on its own.
Table 1 Face sets of the faceted dodecahedra
|
|
|
|
A. 12 faces. Several variations of face can be obtained.
|
|
|
|
|
|
B. 20 faces.
|
|
|
|
|
|
C. 30 faces. Selecting the n edge set forms the well-known compound of five cubes. |
|
|
|
|
|
D. 60 faces.
|
|
|
|
|
|
E. 60 faces.
|
|
|
|
|
|
F. 20 faces. Many variations, including all the self-dual forms and the compounds of |
|
|
|
|
|
G. 12 faces. Several variations, including the great stellated dodecahedron.
|
|
|
|
|
|
H. 60 faces. Dual to the "final" stellation of the icosahedron, or echidnahedron.
|
|
|
|
|
|
J. 15 faces. These are 'hemi' faces which pass through the centre of the dodecahedron. |
|
|
|
|
|
K. 30 faces. These are 'hemi' faces which pass through the centre of the dodecahedron. |
|
Some face planes are divided into regions by edges. In such planes, different edges can be selected to form different faces within the plane, to yield different facettings. Those face sets which do not, on their own, close space to form a polyhedron must be combined with another face set.
Are all such faces allowable? In A, edges n can be selected to form a star pentagon. Alternatively, two adjacent m edges and a single n edge form an obtuse isosceles triangle. Five such triangles form a kind of composite face. Is this face allowable, and why? I make no attempt here to identify or systematize such faces, or to answer this question. Mainly for this reason, the notation used here to describe the faces of facettings is incomplete.
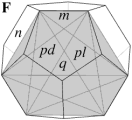
If we create a kind of complete faceted polyhedron including every possible edge and face, then its vertex figure will show all the possible inward structures at a vertex. I will call this complete vertex figure the facetting diagram for the original polyhedron.
The possible edges are those running from one vertex to another, so the facetting diagram will show edges running to all other vertices. The possible face planes are those bounded by three or more coplanar edges. The facetting diagram of the dodecahedron is shown in Fig 3. For reasons of clarity I have not identified the faces.
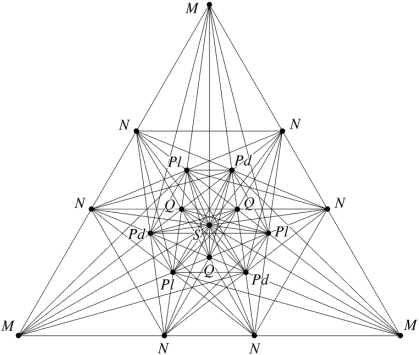
Fig 3 Facetting diagram of the dodecahedron
Note that some features pass through the centre of the diagram and also of the polyhedron. These are edges s and the hemi faces J and K. We will return to these later.
Full stellation diagram of the icosahedron
A stellation diagram shows a face plane of a polyhedron, giving the lines of intersection with the other face planes. These lines define the edges of the various stellations. The points where several lines intersect likewise define vertices.
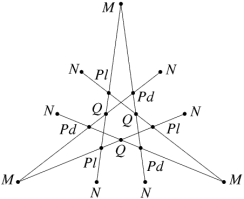
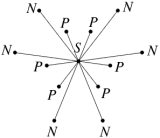
Here is the stellation diagram for the icosahedron as traditionally drawn, with some additional information: I have identified sets of congruent vertices as A to H and sets of congruent edges as m to q (avoiding the letter o). Edges p are divided into dextro (right-handed) and laevo (left-handed) forms, shown as pd and pl respectively. Each set of vertices lies on a circle, which I have also shown (though barely visible in this web version, sorry).
As is often done, vertices H are chopped off the drawing to make more room for the inner detail, and edge segments which extend to infinity are entirely omitted.
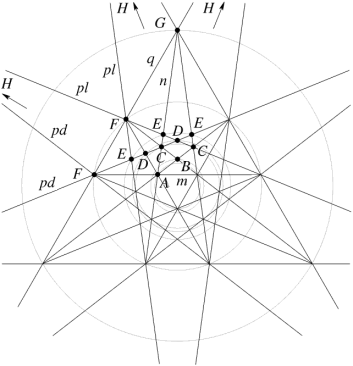
Fig 4 Traditional stellation diagram of the icosahedron
The duality between two polyhedra creates the following reciprocal relationships. I have used the same identifying letter for reciprocal features throughout the diagrams, to help make this clear.
1) The vertex figures of the faceted dodecahedra are dual to the faces of the icosahedra.
2) The face planes of the dodecahedra are dual to the vertex figures of the icosahedra.
3) The edges of the dodecahedra are dual to the edges of the icosahedra, and orthogonal to them.
4) A circuit traced around a face follows the reciprocal sequence of elements (such as mAmAmA) to a circuit traced around the dual vertex figure (MaMaMa).
From these, we find that the stellation diagram of a polyhedron is reciprocal to the facetting diagram of its dual. The stellation diagram of the icosahedron is reciprocal to the facetting diagram of the dodecahedron. Just as the face diagram of a given stellation is a unique subset of the stellation diagram, so the vertex figure of its reciprocal facetting is a unique subset of the facetting diagram. Examples are illustrated in Figs 8 and 9.
In the facetting diagram above (Fig 3), note the point S corresponding to an edge s through the centre of the dodecahedron, also note lines corresponding to 'hemi' faces J, K also through the middle. The reciprocal features of these have been completely ignored in the traditional stellation diagram, because they would have to appear infinitely far from the centre.
Not all polyhedra have finite duals. If a face passes through the centre of the reciprocating sphere, then the corresponding vertex of the dual is located at infinity and the connecting edges describe an infinitely long prism. If we accept both the principle of duality and that hemi solids are polyhedra, we must also accept polyhedra with infinite faces.
Because of this, in the dual figure to the facetting diagram, the lines of intersection between the face planes are in truth infinitely long and end at vertices located at infinity. The traditional stellation diagram is evidently not the full reciprocal of the facetting diagram; it is incomplete. We must find a way to complete it.
Instead of projecting the icosahedron in ordinary flat, 3-dimensional Euclidean space, let us project it in 4-dimensional spherical space. This is rather like drawing a polygon on a ball instead of on a sheet of paper, but with an extra dimension added. Each face, instead of being a flat plane, now lies on the surface of a sphere, and all its lines of intersection are now great circles on the sphere. I will call a line, drawn from the centre of the polyhedron and normal to a face plane, a ray. For a given face, the centre of the sphere must lie on the associated ray, and the sphere will intersect the polyhedron at the vertices and edges of the face. The stellation diagram now comprises closed curves instead of infinite lines, indeed any polyhedron projected in this manner is now finite in size. The diagram is in fact duplicated on the other side of the sphere, so we may conveniently describe only a single hemisphere.
If the above paragraph defeats you, just imagine seeing an ordinary flat stellation diagram through a wide-angle "fish-eye" lens or reflected in a hemispherical mirror. The end result is the same. So now, here is the new stellation diagram, showing the previously missing outer detail. I have in turn had to project the hemisphere onto the plane of this page, which has bent all the lines.
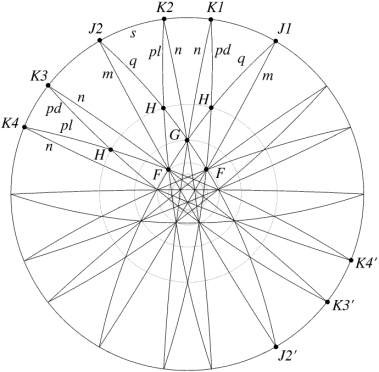
Fig 5 Full stellation diagram of the icosahedron
Edge s is now a circle around the rim, with pairs of parallel edges meeting at vertices J and K along s. The traditional diagram is just the limiting case as the hemisphere's radius increases to infinity. I have numbered the outermost vertices within their sets for identification, as J1, J2, etc.
Notice that each vertex in J, K has two images, one in each direction orthogonal to the reciprocal face plane, but it is still only one vertex. For example J2 and J2' are duplicate images of a single vertex. Infinity can be like that. To see why two images are necessary, consider what happens as a J face of the dodecahedron is displaced sideways. It now reciprocates to a vertex J located far from the centre in the direction of displacement. As J is moved inwards until it reaches the centre, J moves outwards to infinity. As J continues moving off to the other side, J reappears at infinity in that opposite direction and moves inwards. With J in its central position, J is located at infinity, but in which direction? There is no preference. We can only say that it is in both directions at once.
Here is another way to understand the duplicate images. An ordinary (non-hemi) face has two sides, inside and outside. The reciprocal vertex likewise is accessible from both inside and outside. A hemi face J also has two sides, so its reciprocal vertex J should also be accessible from two sides. But each image of J can only be accessed from inside the circle (remember that in our usual Euclidean space, s is located at infinity – there is no outside "beyond infinity"), so there must be a second image to provide access to other side. In this sense you can think of each image as being only half a vertex.
For the serious geometers, duality and reciprocity are theorems of projective geometry. The face plane is now treated as a projective plane projected first onto the projective hemisphere and thence stereographically onto the page, its apparent boundary being a double-image of a projective line. This is the underlying math of the unity of the two vertex images.
Anyway, stellation diagrams now comprise closed curves instead of infinite lines, with some extra vertices and closed regions available to produce extra cells for new stellations (in the case of the icosahedron these are vertices J, K).
Infinite polyhedra
If the centres of the face spheres are located at the centre of the polyhedron, we have a spherical polyhedron which cannot be stellated (though we may draw Schwartz triangles on it). As the centres of the face spheres are moved out along their corresponding rays and their individual radii appropriately increased, the polyhedron changes dramatically and its stellations even more so. A conventional polyhedron in ordinary Euclidean space is seen to be the limiting case as the sphere centres and individual radii go to infinity. Some of the vertices on the face diagrams, and hence some of the stellations, go to infinity too. So we can have infinite stellations. The extra cells appear as endless prisms passing through the core polyhedron and extending to infinity in both directions. The infinite stellations must be included in any complete enumeration of the icosahedra.
Duals of some Stellated Icosahedra
A small selection of stellations and facettings are tabulated here. Their purpose is to help understand what is going on, to see the application of the ideas presented here and to demonstrate and explore some of the problems which they must solve.
Before presenting the table, some explanation of the notations used may be helpful.
Du Val Symbols. Du Val observed [1] that the cell sets form concentric shells around the core. Starting from the core, he labelled each shell in bold lower-case: a, b, c, ...h .
His stellations were not allowed to be hollow, so having a complete shell meant having all the shells inside it too. These solid stellations he labelled in bold capitals: A, B, C, ..., H . Thus B = a + b, etc. (also, A = a).
Some shells comprise more than one shape of cell, for example e has two shapes. These he distinguished by numeric subscripts, for example e1 and e2 . Thus, e = e1 + e2 .
Some shapes of cell come in right- and left-handed forms or enantiomorphs, for example f1. These he labelled in ordinary weight (not bold) type, with the right-handed form (dextro) in normal type, and the left-handed form (laevo) in italic type, for example f1 and f1 . Thus, f1 = f1 + f1 .
A stellation is identified by listing its cell sets in the most economical way, for example De1f1f2 .
In the notation I use elsewhere in this paper, note that there is no relationship with the Du Val cell sets A to H or even a to h, but there is enough similarity in use to confuse the unaware reader. For this reason among others my notation is not ideal, and if you have any suggestions for a better one (which can be easily used on web pages), I would appreciate hearing from you.
Codes. The code number of a stellation is the decimal representation of a binary number obtained as follows:
Because a given cell set is either present or absent, it can be represented by a binary bit, value 1 if present, 0 if absent. Each cell set is assigned a bit in a binary number, starting from the innermost cell as the least significant bit (lsb) and working outwards. The nth bit represents the number 2n, which I call its code number.
So Du Val's shell a = bit 0 (lsb) = code 1, b = bit 1 = code 2, c = bit 2 = code 4, ... , h = bit 11(msb) = code 2048.
The code for a stellation is found simply by adding the codes of its cell sets. Every stellation has a unique combination of bits, and hence also a unique code.
For example De1f1f2 has code 000101011111 = 351 (note the lsb is on the right).
This code number greatly simplified the identification of stellations in my computer programs. For example to examine every combination of cells I could just do a "For n=1 to 4095" (where n is the code).
Since developing this system, I have of course found that analysing cell sets is not helpful in enumerating stellations. However, the system has some advantages. It remains useful for determining the visual appearance of a stellation, is more compact that Du Val's notation, extends naturally to polyhedral stellations with more than 26 cell types, and offers a natural way to order stellations in any list, so it is presented here.
Table 2 The notations compared
|
Du Val |
a |
b |
c |
d |
e1 |
e2 |
f1 |
f1 |
f2 |
g1 |
g2 |
h |
|
Bit |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Code |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
Symbols used for the Faceted Dodecahedra. For the dodecahedra, symbols are either Schläfli's (regular polyhedra), Coxeter et al's [4] (uniform polyhedra), Du Val's (another icosahedron) or a dash (irregular or compound polyhedra).
Table 3 Some stellated icosahedra and their duals
|
Stellated icosahedron |
Faceted dodecahedron |
|||
|
Code |
Du Val |
Description |
Symbol |
Description |
|
1 |
A |
Regular icosahedron {3, 5}. |
{5, 3} |
Face planes A. Regular dodecahedron. |
|
3 |
B |
1st stellation. |
3 | 3 5/2 |
Face planes A, B. 20 triangular and |
|
7 |
C |
Compound of five octahedra. |
– |
Face planes C. Compound of five cubes. |
|
15 |
D |
Isosurtopic (externally similar) to a compound of six pentagonal trapezohedra, but certain vertices are false. |
– |
Isosurtopic to a compound of six pentagonal antiprisms, but with the pentagonal faces removed. |
|
31 |
De1 |
|
– |
Face planes F, B. |
|
32 |
e2 |
Hollow polyhedron. |
– |
Face planes A {5/2}, E. Has internal cavities? |
|
47 |
De2 |
Compound of ten oblate hexahedra. |
– |
Compound of ten trigonal antiprisms. |
|
63 |
E |
|
– |
Face planes E, F. |
|
127 |
Ef1 |
Compound of five tetrahedra (dextro). |
Ef1 |
Compound of five tetrahedra (laevo). |
|
192 |
f1 |
Hollow polyhedron. No conventional way to describe the faces as polygons, because they are only partially filled-in. |
f1 ? |
Self-dual? |
|
255 |
Ef1 |
Compound of ten tetrahedra. |
Ef1 |
Self-dual. |
|
303 |
De2f2 |
12-pointed star. Different internal arrangements of edges can be found, giving different faces. |
3 | 5/3 5 |
These share the same edges, but have differing face planes, respectively A, G and B, G . A third, trimethoric dual is noted in the text. |
|
319 |
Ef2 |
|
– |
Face planes F, G. |
|
511 |
F |
Compound of Ef1 with De2f2. |
– |
Compound of 10 tetrahedra with 3 5/3 5 . |
|
767 |
Ef1g1 |
Isosurtopic to the deltahedron which forms a dimpled dodecahedron, but the dimple vertices are false. |
Ef1g1 |
Self-dual. |
|
1021 |
Fg1 |
Compound of Ef1g1 with De2f2 . |
– |
Compound of Ef1g1 with 3 5/3 5 . |
|
1535 |
Fg2 |
|
– |
Face planes F, G. |
|
2047 |
G |
Great icosahedron {3, 5/2}. |
{5/2, 3} |
Great stellated dodecahedron. |
|
4095 |
H |
Echidnahedron (final stellation). |
– |
Face planes H, i.e. 60 isosceles triangular faces. |
As I investigate the duals, unexpected findings are emerging. Our current understanding of polyhedra in general is surprisingly incomplete. For example, we have seen there are infinite stellations. Here are some more findings, presented with illustrative example polyhedra. The example stellations are identified by Code number, followed on first mention by the Du Val symbol in parentheses.
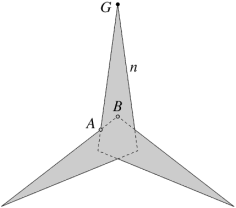
Stellation 303 (De2f2) is a simple and beautiful 12-pointed star, see Fig 6. Its Du Val symbol, based on its cell sets, seems inappropriate and clumsy. Another problem is that it has at least three dual facettings (see Table 3), depending on the way its internal structure is chosen. Evidently several different stellations, each dual to one of those facettings, must have the same external appearance and differ only in their internal structure. This stellation neatly demonstrates the inadequacy of using cell sets or external faces to describe stellations and their reciprocal facettings.

|
|
|
Fig 6 303 (De2f2) and its face diagram. Different internal structures are possible, two are indicated by the alternative vertices A or B and dashed lines. |
|
George Olshevsky has suggested the word "isosurtopic" to describe polyhedra which are externally similar; after the surtope – the polyhedron which is formed by the external regions only. We may note that [1] confined itself to surtopes of the stellated icosahedra.
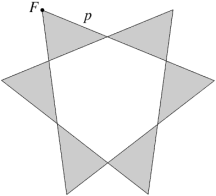
Stellation 192 (f1) is a hollowed-out polyhedron, see Fig 7. It can be thought of as those cells, from the compound of ten tetrahedra, which belong to only one tetrahedron. Each face is bounded by two overlapping triangles, i.e. it has six edges and six vertices (as with the compound of ten tetrahedra), but with the inner region hollow to allow access to the central cavity of the polyhedron.

|
|
| Fig 7 192 ( f1) and its face diagram | |
192 is also a facetting of the dodecahedron, so its dual must be another stellation of the icosahedron. Its face and vertex figure are congruent. These observations are consistent with it being self-dual. Just possibly its dual is a different polyhedron which is also both a stellation of the icosahedron and a facetting of the dodecahedron and has congruent face and vertex figure dual to those of 192. How can the answer be found and proved?
Traditional polygon theory is not really concerned with holes – regions inside the bounding edges are inside, whether they are filled or not. A prison makes a nice analogy; traditionally, a prisoner is held captive whether they are under a roof inside a building or in the open air such as in a walled compound. But when the two-dimensional polygon is used as the face of a three-dimensional polyhedron, the holes do matter; just as a prisoner with a ladder or a friendly helicopter can climb into the third dimension and escape from the compound, but not from their cell. So traditional polygon theory does not adequately describe the faces of 192. (At least, I am not aware of anything in the literature. Some work on toruses comes close, but I have found nothing useful in this context.) Any attempt at modifying the polyhedron to allow a conventional description requires additional vertices, which in turn forces additional edges (this is seen clearly through consideration of the dual), resulting in different, n-methoric faces (see below) and a different polyhedron.
Another hollow stellation, not illustrated here, is 32 (e2). If we attempt to construct its dual facetting, we find the interior divided into many regions by intersecting faces. The otherwise identical solid facetting is a dual of 47 (De2), so we may conclude that the dual of 32 is distinguished by being hollow. This implies one or more fully enclosed interior cavities. Traditional theory defines a polyhedron by its vertices, edges and/or faces, but offers no way to decide which interior regions are solid and which are hollow and hence distinguish these two facettings.
These polyhedra, namely 192, 32 and their duals, demonstrate that we actually need to extend current theory to cope with holes. Generalising to p dimensions: for the general p tope (p dimensional polytope), p-1 dimensional holes in its outer surface have a dramatic effect on the p tope, but internal p dimensional holes have no visible effect (a 2D flatlander cannot from outside see the hole in a face of 303) and so up to now have been treated as trivial. Their importance only becomes apparent when you use the p tope to construct p+1 topes.
I have called polyhedra with three faces meeting along an edge 'trimethoric', and those with three vertices distributed along an edge 'trisynaptic' [5]. One may extend the idea generally to polyhedra with n faces or vertices at an edge, as n-methoric and n-synaptic. Many n-methoric and/or n-synaptic facettings can be found; their dual stellations are also trisynaptic and/or trimethoric.
|
|
| Fig 8 Face A and vertex figure of a trimethoric facetting | |
The facetting shown in Fig 8 has faces A, E and G, where faces A are star pentagons and faces G are convex pentagons. Edges n are trimethoric. The dual of the vertex figure gives the face of the reciprocal stellation, see Fig 9. The trisynaptic structure is visible on the outer surface of the polyhedron, which happens to be yet another variant of 303. Traditional theory only recognises even numbers meeting, not threes or other odd numbers. We must again extend traditional theory, either to accept that these constructions are some kind of polyhedra, or to define them as something else.
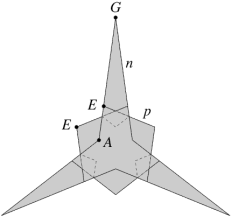
|

|
|
Fig 9 Face and 3D view of a trisynaptic stellation. The dashed lines show the boundaries of the visible regions. |
|
Conclusion – untidy polytopes and precursors
The extensions to traditional theory mentioned above should not prove too difficult. However, the various unconventional polygons and polyhedra described here are probably of relatively narrow interest: much of polytope theory is rightly concerned with the more tidy mathematical properties of the well-studied polytopes. A useful umbrella term for these unconventional types would be "untidy" polytopes. More conventional polytopes would naturally be "tidy." Among the well-known polyhedra, the hemi ones and some of the stellations which obey Miller's rules are untidy. The untidy features we have come across here (there are probably others) may be collected and generalised:
- Hemi elements, passing through the centre.
- Infinite elements, reciprocal to the hemi elements.
- Holes.
- n-methoric and n-synaptic edges.
Stellations are traditionally enumerated by examining either the possible cell sets or the face regions visible on the outside. However, neither of these approaches has an obvious reciprocal method for enumerating facettings.
Clearly we need a new approach which does reciprocate rigorously. If we select elements from the facetting diagram to create vertex figures of facettings, this method reciprocates exactly with selecting elements from the stellation diagram to create face diagrams of stellations. In general such vertex figures do not reciprocate exactly with externally visible face regions; that is, the stellations so enumerated will in general have an internal structure. This fits in well with our current understanding of polyhedra.
This essay has made extensive use of the fact that, through reciprocation, the definition of one polyhedron also rigorously defines another. One might suggest that the two polyhedra can be thought of as different realizations of the same mathematical object. That is, a single mathematical representation, or precursor, might be used to define both polyhedra. For example, if certain elements of the precursor are designated as faces then one polyhedron is realized, but if they are designated as reciprocal vertex figures then the dual polyhedron is realized. Or, {3,5} and {5,3} could be thought of as different element orderings of the same precursor. It remains to be seen whether the idea of such precursors has any value. (I have subsequently learned that such precursors are known as abstract polytopes and they are of much wider theoretical importance).
The perfect symmetry of the dual relationship has proved a powerful idea in understanding the nature of the stellated icosahedra and faceted dodecahedra. However before we can go on to enumerate the stellations of polyhedra such as the icosahedron, there is still some work to be done in formally extending polygon and polyhedron theory to allow for various kinds of untidiness.
Acknowledgements
My thanks are due to several members of the polyhedron community, who have helped me with ideas for, and corrections to, the terminology used here. Robert Webb, creator of Great Stella, deserves special mention for bringing me down to earth when I needed it (although I have yet to try its new features, Great Stella for MS Windows looks ideal for investigating both stellation and facetting [3]).
The illustrations were prepared with the help of !Stellate and !PolyDraw software from Fortran Friends, fortran.orpheusweb.co.uk. To run these programs you need the operating system RISC OS 3.1 or higher. For this you will need either an Acorn compatible PC, or a standard MS Windows PC running VirtualAcorn from www.virtualacorn.co.uk.
References
[1] H. S. M. Coxeter (et al), The fifty-nine icosahedra, 3rd Edition, Tarquin (1999).
[2] G. Inchbald, In search of the lost icosahedra, Math. Gaz. 86 (July 2002) pp. 208-215.
[3] R. Webb, Stella: polyhedron navigator, Symmetry: Culture and Science, elsewhere in this issue.
[4] H. S. M. Coxeter (et al), Uniform polyhedra, Phil. Trans. 246 A (1954) pp. 401-450.
[5] G. Inchbald, Trimethoric (and trisynaptic) polyhedra, Mathematics and Informatics Quarterly 2/2001, Vol 11, pp. 71-74.