The Archimedean Honeycomb Duals
Updated 4 March 2019
This article is substantially reproduced by kind permission from:
Inchbald, G.; "The Archimedean Honeycomb Duals", The Mathematical Gazette 81, July 1997, p.p. 213-219.
A comment on symmetry has been added near the end, and a few other minor corrections and clarifications made.
Introduction
The first part of this article covers some well-known ground in preparation for the second part on the Archimedean honeycomb duals. Mathematically speaking some of this second part is, so far as I know, no more than conjecture: I do not myself know of a proper systematic approach to such honeycombs.
As far as possible I have used names for the polyhedra from standard references (e.g. [1]). But references vary, and I have not found all of them described. In such cases I have tried to choose names which are appropriate and technically correct.
Honeycombs and duals
Polyhedra which can be packed together periodically, to fill space exactly with no gaps, may be thought of as cells in a space-filling honeycomb. Uniform polyhedra have regular faces and isogonal vertices (congruent and forming a single symmetry group); the convex ones are known as the Archimedean polyhedra, which for our purposes include the uniform prisms and the fully regular Platonic polyhedra. Some of them can be packed in various ways to give a family of uniform honeycombs (e.g. [2]), with isogonal vertices as well as regular faces and uniform cells. Because their cells are all Archimedean polyhedra, I call them the 'Archimedean' honeycombs.
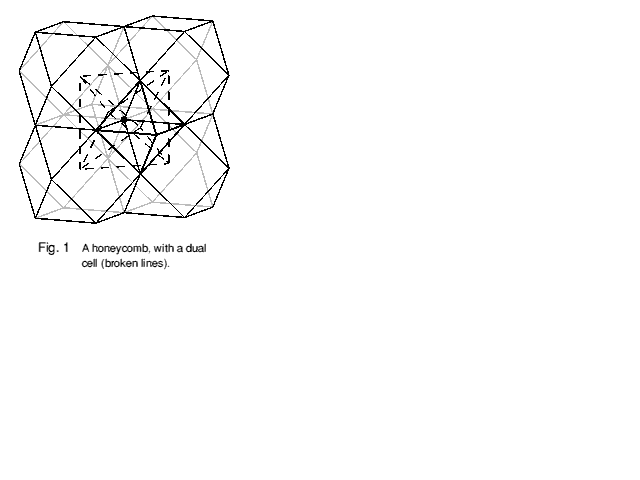
The cells of a honeycomb need not all be alike: the packing shown in Figure 1 has four cuboctahedra and two octahedra sharing a common corner point or vertex (identified by a dot). The shape in broken lines will be explained later.
 |
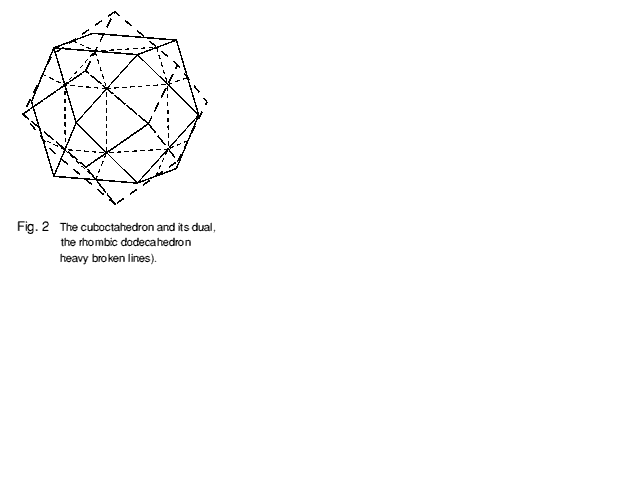 |
To understand what a dual honeycomb is, it may be easier to start with dual polyhedra. Every polyhedron has a reciprocal or dual polyhedron whose faces correspond to vertices of the original, and whose vertices correspond to its faces. They both have the same number of edges, with each original edge having a dual edge at right angles to it. For example the cuboctahedron in Figure 2 has 14 faces and 12 vertices, so its dual the rhombic dodecahedron (shown in broken lines) must correspondingly have 14 vertices and 12 faces. An Archimedean polyhedron has regular but differing faces and isogonal but non-regular vertices, whereas its dual has isohedral (congruent and forming a single symmetry group) but non-regular faces and regular but differing vertices, as can be seen in Figure 2. With any dual, the process is reciprocal: this just means that if we construct the dual of a dual we get back to the original.
Duality occurs in higher dimensions too. The general straight-sided 'solid' in n dimensions is called a polytope, and as it happens a honeycomb in n dimensions may be regarded as a degenerate polytope (of infinite radius) in n + 1 dimensions. So to find the dual of a 3-D honeycomb, we must treat it as a 4-dimensional polytope!
The rules for doing this are somewhast simplified for uniform figures and are actually not too bad if we don't think about where they come from. The dual of a honeycomb has a vertex at the 'centre' of each original cell, and a cell around each original vertex. Edges of the dual pass through each original face, and faces likewise lie across edges. I qualify the word 'centre' here as a cell may be asymmetric, making its effective centre difficult to define. In the example honeycomb shown in Figure 1, an oblate octahedron is shown in broken lines: it has the common vertex at its centre and forms a cell of the dual honeycomb.
For a uniform honeycomb, a more rigorous definition of its dual is illustrated by the idea of a vertex figure. Taking a vertex of the honeycomb as a reference, we first find the mid-points of all the edges which end at the reference vertex. These points are the vertices of a new polyhedron which has the reference vertex at its centre, and is called the vertex figure. We then find the (3-D) dual polyhedron to the vertex figure. This turns out to be the same shape as a cell of the dual honeycomb, though not necessarily the same size. Put concisely; the cells of the dual of a uniform honeycomb are isomorphous with the dual of the vertex figure of that honeycomb.
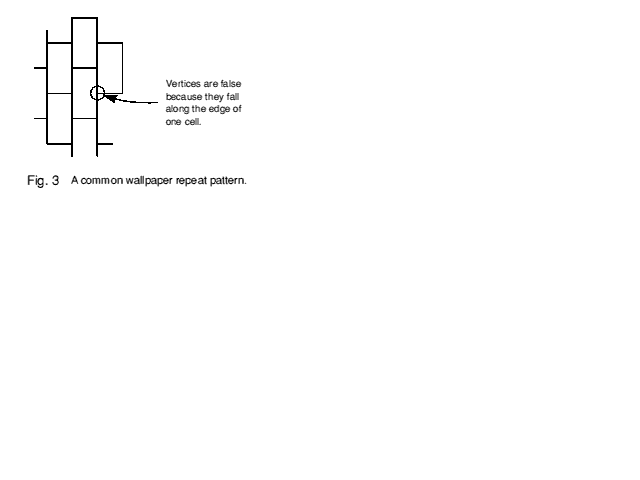
Any packing with 'false' edges does not have a dual (and by reciprocation cannot be a dual), and is not a true honeycomb. A false edge is one where at least one adjacent cell has a coincident edge, and at least one adjacent cell does not, for example an edge of one cell may fall across a face of another. The equivalent in 2 dimensions are false vertices: the rectangular repeating unit of Figure 3 commonly used for wallpaper is an example. False vertices can also appear in 3-D packings but are always accompanied by false edges, although false edges may occur without false vertices.
The family of Archimedean honeycomb duals
The family of Archimedean honeycombs can be divided into two groups, namely simple packings of prisms in stacked layers and more complex packings involving the main Archimedean polyhedra. I am not concerned here with the simple prism packings, but with those of the main polyhedra. Each such honeycomb has from one to four distinct cell types, and, like the component polyhedra, has isogonal vertices. The corresponding family of their duals is less well known, and is the subject of this investigation. I will call these the Archimedean honeycomb duals.
Just as the dual of an Archimedean polyhedron has isohedral but non-regular faces, so the dual of an Archimedean honeycomb has isogonal but non-regular cells. The Archimedean honeycombs are listed in Table 1 together with identifying symbols and the cells of their corresponding duals. The types of cell and the number of each type surrounding a vertex define an Archimedean honeycomb, and correspond exactly with the types and number of vertices of the dual cell.
TABLE 1 The Archimedean Honeycombs and Dual Cells
My Symbol |
Cells Surrounding a Vertex |
Cell of Dual |
|
| No. | Type | ||
| C | 8 | Cube | Cube |
| TO | 4 | Truncated octahedron | Disphenoid tetrahedron |
| O+T | 6 8 |
Octahedron Tetrahedron |
Rhombic dodecahedron |
| T+TT | 2 6 |
Tetrahedron Truncated tetrahedron |
Rhombic hexahedron |
| CO+O | 4 2 |
Cuboctahedron Octahedron |
Oblate octahedron |
| O+TC |
1 4 |
Octahedron Truncated cube |
Oblate square pyramid |
| OP+TCO | 2 2 |
Octagonal prism Truncated cuboctahedron |
Characteristic tetrahedron |
| C+CO+RCO | 2 1 2 |
Cube Cuboctahedron Rhombicuboctahedron |
Skewed trigonal dipyramid |
| C+TCO+TO | 1 2 1 |
Cube Truncated cuboctahedron Truncated octahedron |
Trirectangular tetrahedron |
| C+RCO+T | 1 3 1 |
Cube Rhombicuboctahedron Tetrahedron |
Asymmetric trigonal dipyramid |
| CO+TO+TT | 1 2 2 |
Cuboctahedron Truncated octahedron Truncated tetrahedron |
Rhombic pyramid |
| TC+TCO+TT | 1 2 1 |
Truncated cube Truncated cuboctahedron Truncated tetrahedron |
Monorectangular tetrahedron |
| C+OP+RCO+TC | 1 2 1 1 |
Cube Octagonal prism Rhombicuboctahedron Truncated cube |
Rectangular square dipyramid |
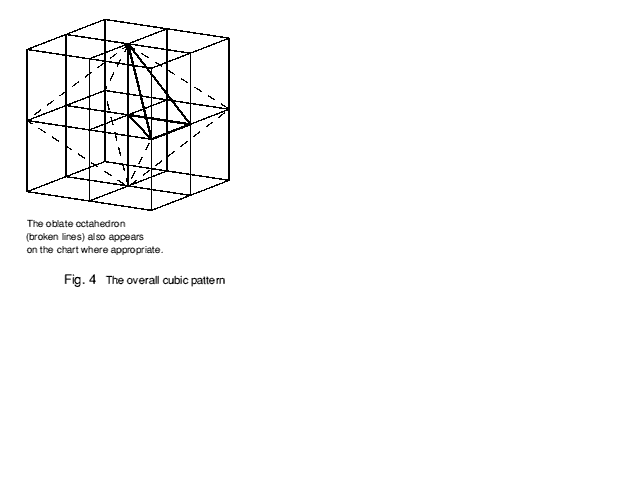
I now take a short detour to look at one way in which space can be carved up; but we will find that it is not really a detour. Any planar polygon may be divided up into right-angled triangles. Similarly, any solid polyhedron may be divided up into tetrahedra with three mutually orthogonal edges connected in a kind of 3-D zigzag: the tetrahedron heavily outlined in Figure 4 is an example. If the three orthogonal edges are all the same length then the tetrahedron may be thought of as the 3-dimensional equivalent of an isosceles right-angled triangle, and is called the characteristic tetrahedron of the cubic packing. Look closely at the one heavily-outlined in Figure 4, and you will see that it is 'handed', i.e. it has a mirror-image twin. Packed alternately, these two characteristic tetrahedra fill space.
 |
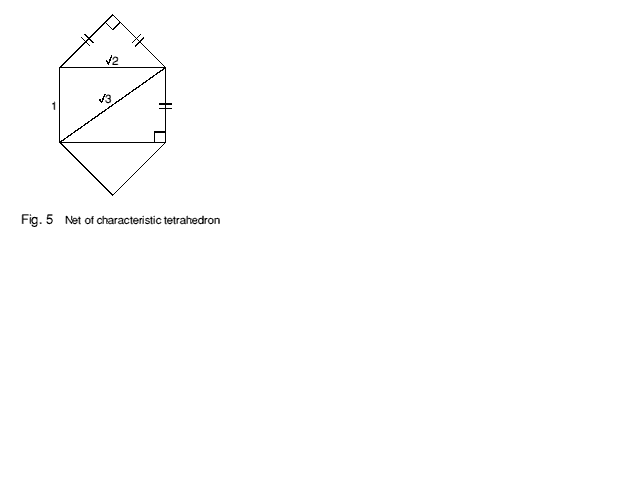 |
If we take a twin pair of characteristic tetrahedra we can join them together in different ways, depending on which isohedral faces we put together, to make new shapes. Several congruent new shapes can then be grouped symmetrically together around a common face, edge or vertex to form another new shape, and so on. We could follow various routes, some interweaving, until eventually we can build up a family of polyhedra. Figure 4 illustrates how the basic pattern fits an overall cubic symmetry. It is instructive to make models from card and fit them together to make up the possible shapes. The net of the characteristic tetrahedron is shown in Figure 5: others may be found by travelling the path for oneself.
I recently came across a puzzle made from twelve characteristic tetrahedra, with alternate left- and right-handed forms linked end to end by fabric hinges to form a ring: scalene faces are moulded in purple plastic and isosceles faces in green. Many of our shapes can be made by manipulating the ring, which comes packaged as an asymmetric trigonal dipyramid.
To give the process a sensible direction, we need to make up some rules on what is allowed. First, we will stick only to symmetrical arrangements which form convex polyhedra with no 'dips' in their surface: we then appear to find that every shape we can make is a space-filler. We rule out larger copies of shapes we have already made (with one possible exception to be mentioned later). We retain overall cubic symmetry, so the honeycomb looks the same whether viewed from above, the front or the side. Finally we confine ourselves to those shapes which form true honeycombs with no false edges. Our family of polyhedra now appears to be finite, and ends with constructing either a cube or a rhombic dodecahedron.
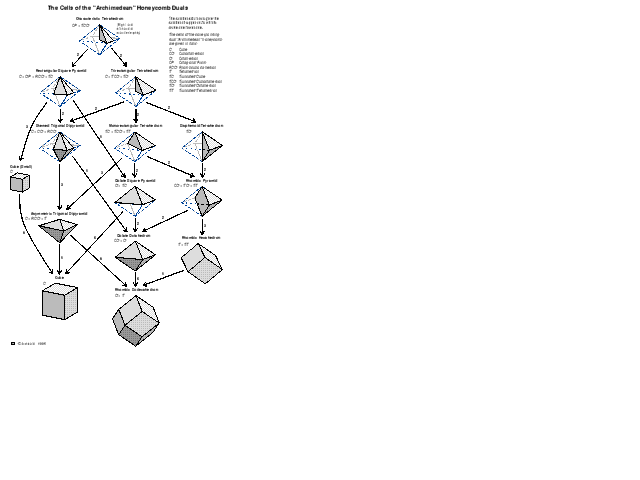
The family and their relationships are illustrated on the accompanying chart. The names on the chart may need some explanation, though I hope most are clear enough. 'Sphenoid' means wedge-shaped, 'oblate' means flattened (like a beachball someone is standing on), 'trigonal' is triangular, and 'rectangular' means it has a right angle. The truncated cuboctahedron is also known as the great rhombicuboctahedron, and the oblate octahedron as a square dipyramid. You may notice that some apparently possible shapes are missing from the chart: this is because they do not meet the conditions defined above.
 |
To view a larger, more legible version of the chart, click here. To download a printable PDF chart, click here. |
The family is found to have an unexpected property in that it appears to be the family of cells of the Archimedean honeycomb duals: every member of the family described is the cell of a dual, and every Archimedean honeycomb is represented. Unfortunately, as mentioned in the introduction, I have not been able to find a formal proof (or disproof) of this conjecture.
To finish off, a few observations on the chart may be made. The packing of the cube C is the only perfectly regular one. Its dual must also be regular, so it must be self-dual (like the tetrahedron in 3 dimensions). Hence its presence among the duals even though it is an Archimedean. C occurs twice on the chart in large and small sizes, which technically breaks one of the rules laid down earlier: this stems from the geometrical way the large cube is divided up to obtain other members of the family (see Figure 4).
A figure having all faces alike within its overall symmetry is said to be isohedral. The only Archimedean honeycomb besides C with this property is O+T. It is said to be quasi-regular, and its dual has rhombic dodecahedral cells. The two regular and quasi-regular honeycombs, C and O+T, are distinct end points of the series. If we consider the isohedral duals, there are four; C and OT as before, plus also CO+O and T+TT. These are the four lowest members of the series. They are dual to the four Archimedeans having all edges equivalent within the overall symmetry. All this suggests that the series represents an increasing order or symmetry as it progresses, with the characteristic tetrahedron and OP+TCO having the lowest symmetry of all, and the bottom sets the highest.
Other notable Archimedeans do not appear to have similarly notable duals, and vice versa. TO is the only one besides C to have congruent cells, but its dual occupies an undistinguished place in the third row. Only one Archimedean, C+OP+RCO+TC has four cell types, but its dual lies equally obscurely in the second row. One might perhaps expect that the Archimedean which is dual to the characteristic tetrahedron would be notable in some way; it is OP+TCO which seems quite ordinary.
Acknowledgements
The 3-D views of polyhedra were created by WimpPoly and Polydraw software from Fortran Friends, PO Box 64, Didcot, Oxon OX11 0TH. I am indebted to the author K. M. Crennell for advice, enthusiasm and pre-release software.
References
[1] H.S.M. Coxeter, Regular Polytopes, Dover, New York (1973).
[2] R. Williams, The Geometrical Foundation of Natural Structure, Dover, New York (1976).
Bibliography
K. Critchlow, Order in Space, Thames & Hudson, London (1976). This is a very visual investigation but not rigorous.
H.M. Cundy and Rollett, Mathematical Models, OUP, London (1961). Chapter 3 gives a gentle introduction to polyhedra and duality.
Chapters 4 and 7 of [1] cover systematically the more regular honeycombs.
Chapter 5 of [2] illustrates the Archimedean honeycombs.