Is There a Self-Dual Hendecahedron?
Recent change history
26 Feb 2023: More cleanup.
13 Feb 2021: Cleanup, minor additions.
Duality
The principle of duality states that for every polygon there is a dual, or reciprocal, polygon, whose edges correspond to the corner points (vertices) of the original and whose vertices likewise correspond to its edges. Similarly in three dimensions, for every polyhedron there is a dual, or reciprocal, polyhedron, whose faces correspond to the vertices of the original and whose vertices correspond to its faces. The principle is well known - for duals of many common polyhedra, see [1].
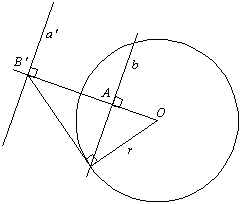
Figure 1 Reciprocation
To obtain the dual of a polyhedron, a common method is to reciprocate it with respect to a concentric sphere. The reciprocal figure is then dual to the original. If this duaL is then reciprocated again in the same sphere, the original polyhedron is recovered.
In Figure 1, A and B' are vertices. For polygons, a' and b are edges. For polyhedra, a' and b are sections through faces, and the circle is a section through the reciprocating sphere.
A and a' are reciprocal. For a polygon or polyhedron with vertex A, its dual has an edge or face a'. Likewise b and B' are reciprocal. Note that:
OA . OB' = r2.
For r = 1, OA = 1 / OB'
i.e. the lengths OA and OB' are reciprocal.
Not all polygons or polyhedra have an unambiguous centre. For example a square pyramid does not. In such cases it is convenient to use the centre of gravity (mean position) of the vertices. (In fact not all polygons and polyhedra have finite standard duals, see for example [2]. As described here and often elsewhere, the principle of duality has been oversimplified, but that need not concern us here.)
Self-duality
If a regular polygon is reciprocated with respect to a concentric circle of appropriate radius, a congruent polygon is obtained and the polygon is said to be self-dual. For a polygon of radial distance v to each vertex and e to each edge, the radius r of the circle is given by:
ve = r2.
More generally, irregular polygons which are self-dual also exist. For example some parallelograms are self dual (to mirror reflection).
A few polyhedra are also self-dual, i.e. the dual is congruent to the original. Examples are to be found in the family of pyramids, including the regular tetrahedron. In a self-dual polyhedron the vertices and faces have a one-to-one correspondence, so it must have the same number of each (e.g. four in the case of the regular tetrahedron). Another characteristic involves the vertex figures: for our purposes, a vertex figure is the polygon formed by the cut surface when a given vertex is sliced off. For self-duality, the faces and vertex figures have a particular correspondence, in that each vertex figure is the dual polygon of the corresponding face.
To ensure that the dual is the same size as the original, the centre and radius of the reciprocating sphere must be carefully chosen. For the regular tetrahedron the intersphere is used, which is the sphere having its centre at the same point as the tetrahedron and tangent to the edges at their mid-points. The compound of two regular tetrahedra in such a dual relationship is known as the stella octangula (which is Latin for an eight-pointed star).
The hendecahedron
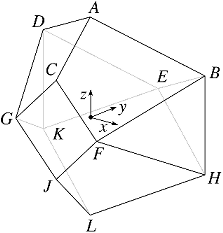
Figure 2 The bisymmetric
hendecahedron
Many years ago [3] I came across a certain hendecahedron (an eleven-sided polyhedron). By distorting (morphing) it I obtained different versions (isomers) with different characteristics. The most symmetrical was the bisymmetric hendecahedron shown in Figure 2 and in more detail here, so called because it has two planes of symmetry.
It was pointed out to me by Kate and David Crennell that the hendecahedron has the same number of vertices, 11, as faces. On checking this observation for myself I saw that, furthermore, the vertex figures and faces had the basic correspondence required for self-duality. The two planes of symmetry are interchanged in the reciprocal figure, so that it stands on edge, and the it is also oriented back to front. For example the face CGJF reciprocates to a vertex congruent to E and located a little outwards from CGJF, and likewise the vertex E reciprocates to a face congruent to CGJF and located a little inwards from E.
But in the hendecahedron shown, the vertex figure of E has the wrong proportions to be the planar dual of CGJF – it is rectangular, whereas the dual of CGJF is square. Is it possible to distort the polyhedron into a version with the correct proportions to be self-dual? And what are the location and radius of the reciprocating sphere? Or are there a whole range of self-dual arrangements, or none?
Approaches to the problem
There are two possible approaches to the problem, analytical or numeric. Either way, the fact that the polyhedron has two planes of symmetry allows the problem to be simplified a little – the solution to part of the polyhedron may be found and then by symmetry applied to the remainder of it.
Analytically, where each of the planes of symmetry bisects the polyhedron, the cut face is a pentagon. Because the two planes are interchanged by the reciprocation, for self-duality these pentagons must be planar duals of each other. However, I do not think they will be regular. This was as far as I was able to take my own analysis.
Numerically, the best approach seems to be successive approximations. I would suggest the following algorithm:
(1) Guess the answer,
(2) Find its dual, by reciprocating with respect to a sphere of radius 1 and centre 0,0 as in steps (a) to (e) below,
(3) Take a polyhedron intermediate between the two (I am not sure of the best way to do this. The important thing is to ensure that the faces are flat),
(4) Use this as the next guess,
(5) And so on, until the difference between successive guesses is suitably small.
The first guess must be reasonably close (e.g. vertices and faces in a correct relationship to the reciprocating sphere). Different guesses could be tried, to see whether they all find the same solution or a range of solutions.
To find the dual of a polyhedron, I would suggest:
(a) For each vertex, find the equation of the radius joining the centre to the vertex,
(b) If the distance of the vertex from the centre is v and r = 1, then the distance of the reciprocal plane from the centre = 1/v ,
(c) The plane is orthogonal to the radius, so its equation can now be found,
(d) The line of intersection between two planes is the line in which their common edge lies,
(e) The point of intersection between three or more edges is a vertex of the dual polyhedron.
This was as far as I got with a numerical approach. I was unable to solve the problem either way, though obviously an analytical solution is preferable. In fact, the general problem has been solved for at least one solution.
The canonical form
The solution just mentioned is called the canonical form of the polyhedron. This form has an intersphere such that every edge is tangent to it, the sphere centre is the centre of gravity of the tangent points, and every edge of the dual polyhedron shares the same tangent points. It is a theorem that every convex polyhedron can be morphed into such a form, which has earned it the title "canonical". The reciprocal with respect to the intersphere is known as its canonical dual.[4]
If the dual pair are congruent, then the canonical form is self-dual. Conversely, if a polyhedron is self-dual then its canonical dual will be congruent. The canonical hendecahedron turns out to be one such example.
But is the canonical figure the only solution? For example the canonical quadrilateral is the square, yet other self-dual quadrilaterals exist. Might there be other hendecahedral morphs where the dual figures are congruent but not canonical?
References
[1] Cundy, H.M. and Rollett, A.P.; Mathematical Models, OUP, 1961.
[2] Wenninger, M.; Dual Models, CUP, 1983.
[3] Inchbald, G.; "Five Space-Filling Polyhedra", The Mathematical Gazette, 80 (1996), 466-475.
[4] Hart, G. W.; "Calculating Canonical Polyhedra." Mathematica Educ. Res. 6, 5-10, Summer 1997.