^Top

Polytopes: Degeneracy and Untidiness

Updated 5 Apr 2023

This essay is unfinished and still very much a work in progress. In fact most of what I wrote earlier is proving unsound and I have been rethinking its focus.

Recent changes

11 May 2022. Beginning a second major rethink of the article focus.

10 Feb 2019. Abstract theory linked in. Much revised terminology. Other improvements.

9 April 2005. Precursors renamed from generators. Odd bits improved and a note on a forthcoming essay added, as much to show that I am still making progress on the current topic as for any other reason.

Contents

Degeneracy and untidiness

The theory of polyhedra has been evolving for over two thousand years, ever since the ancient Greeks discovered the five Platonic solids. For most of that time everybody knew what a polyhedron was, and sought to develop the theory around their intuitive ideas. However as time went by and elegant theories such as Euclidean geometry and Eulerian stereometry arose, there always seemed to be degenerate polyhedral forms which didn't fit. The rise of non-Euclidean geometries and Poincaré's analysis situ resolved some puzzles but also brought new and deeper ones. By the twentieth century, definitions of a polyhedron were multiplying to try and accommodate every theorist's ideas, be they linear programming, topological analysis, or combinatorial set theory. The difficulties multiplied with the theories. Each field learned which polyhedra did not fit its theories and labelled them degenerate. Theorists confined themselves to the ones that did fit, because thet exhibited what I call a tidiness of form, within their theoretical model. But no two fields could agree any more on what a polyhedron was, never mind which examples were tidy or degenerate. Everything was becoming inconsistent with everything else.

I suggest here that the two aspects, of tidiness and of theory, interacted together to create this unhealthy state of affairs. Investigators grabbed ideas that interested them intuitively and tried to put theoretical form to them. All too often the results did not match the intuitions; when pushed to their logical conclusions, the theories produced degenerate or untidy figures. Some theorists simply walled the untidiness out of their minds and applied their theory only to the tidier polyhedra that did interest them. Others reponded by developing a new intution about the discrepancy and brewing up a new theory around it. Every theory led to new kinds of untidiness, and every degeneracy led to new theories in the attempt to eliminate them. The quest for tidiness became an endless cycle of burgeoning confusion. As mathematicians, theorists should be using their theories to shape new and rationally-based models for their intuitions. However all too often it has been the other way round and theorists have used their intuitions to shape new and irrationally-conceived theories.

Certain recent developments, such as abstract polytopes and my own morphic theory, have brought some insights into all these clashes of ideas. However my purpose here is not to resolve these clashes but to highlight their existence and nature. If you are more interested in the nature and outcome of that resolution, then check out my essays on Morphic Polytopes and Dualising polyhedra.

The term "polyhedron" has been applied to a wide variety of three-dimensional forms. A polyhedron-like structure which does not conform fully to the more standard definitions is sometimes said to be degenerate. However, different authors' ideas of what is standard and what is degenerate tend to differ. This difference is partly due to their differing areas of interest, and partly due to a failure to separate geometric and topological properties. That is to say, traditionally a degenerate structure may have a degenerate topology, such as my Trimethoric (and Trisynaptic) Polyhedra. Altyernatively, it may have a well-formed topology but degenerate geometry; the regular dihedra {n 2} and hosohedra {2 n} are typical examples of this, being valid topological or even spherical polyhedra, but degenerate when their faces are flattened. Notice that if the topology is degenerate, the geometry can sometimes still appear valid; for example topologically we may duplicate a face of a cube such that its bounding edges are trimethoric, but then inject it into Euclidean space with flat faces, so that the rogue face is coincident with the original and it appears to be an ordinary cube.

Johnson noted this difficulty and proposed that "degenerate" should be reserved for abstract incidence complexes which are not properly formed abstract polytopes, for whatever reason (the mutant cube just described is an example of this). For a malformed geometric realization of a true abstract polytope, he suggested the term "reductive" (see Polytopes - Abstract and Real), though the term "unfaithful" is more common. But some malformations, such as curved elements, are not really reductive, just different. I use the term "untidy" in order to make the direct contrast with the accepted or tidy forms.

Both Johnson and I have independently made the point that ideas of what is or is not reductive or untidy vary widely depending on the particular geometer's area of interest, and that it is therefore a key aspect of such terms that the exact meaning is subjectively defined or, at best, defined locally within the specific context under discussion.

Some common examples in Euclidean space of features which we might think of as untidy include:

Curiously, while many authors have described polyhedra having one or more of these untidy properties, a planar figure exhibiting any equivalent properties is seldom accepted as a polygon. For example a quadilateral with curved sides may be accepted as a polygon when drawn on a sphere but not when drawn in the plane. There is a lack of consistency in this tradition, which requires cleaning up.

Overlapping or coincident features

Star polygons whose boundaries cross over themselves are almost as old as their convex cousins. The star pentagon or pentagram was sometimes adopted as a mystical symbol, not least by the Pythagorean cult of Classical Greece. Around two thousand years later Renaissance artists liked to fashion star polyhedra from them, with Kepler first noting two of the regular star dodecahedra. Poinsot noted their duals. Nobody was really troubled by the overlapping or crossing regions of these self-intersecting figures.

If a polyhedron has two colinear but separate edges, its geometric reciprocal may have these edges superimposed such that four faces meet at the combined edge. For a geometric polyhedron this is traditionally not allowed, or at best regarded as degenerate (though there is of course some debate). Note however that combinatorially it will retain the two distinct edges of the original, and remains well-formed. Consequently we may now understand such forms as Skilling's Great disnub dirhombidodecahedron to be genuine polyhedra, albeit having an untidy appearance.

Curved faces

Yet another class of geometrically untidy polyhedra are those with non-planar faces. Here, the edges of a face typically form a skew polygon, and may or may not be straight. Any combinatorial polyhedron may be represented by a simply-connected graph [2]. A circuit enclosing any region of the graph represents a face - a circuit around an irreducible region represents a face of the outer hull, and a wider circuit around several such regions represents an edge facet of that hull. Combinatorially this is all nice and tidy, but geometrically the general circuit is skew, leading to skew facets; it is only in certain special cases that the circuit and facet are planar.

The skew facets may be thought of in different ways, as empty in the manner of Grünbaum, as filled with a curved minimal surface such as found in certain theoretical bubbles or saddle polyhedra [4], or as filled with some other specialised surface such as the walls between real bubbles of different sizes, in a foam. Bubbles tend also to have curved edges. One may also observe that there are a large number of facetings of a typical polyhedron, of which only a relatively small subset have planar faces. The question arises as to whether the non-planar cases reciprocate to any meaningful polyhedra. If a general curve is treated as a string of arbitrarily short line segments joined by vertices, then its reciprocal is seen to be a string of vertices joined by arbitrarily short line segments, which is a similar construction, viz. another curve. [No doubt the theory of reciprocal curved lines and planes goes a lot further. If reciprocation does break down, how do we account for the dual structure? If not, what is the reciprocal of a bubble?]

Features at infinity

In Euclidean space, if a face plane passes through the centre of the reciprocating sphere then the face reciprocates to a vertex located at infinity, i.e. one which has no place in Euclidean space. The incident vertices reciprocate to infinite prisms. Combinatorial duals of such "hemi" forms, and even geometric reciprocals in elliptic or projective space, cause no such problems.

The hemi faceted cube has six "butterfly" cross-quadrilateral faces and three rectangular hemi faces. The crossing points in the middle of each cross-quadriateral are "false vertces," i.e. there is only the illusion of a vertex. This cube is unusual in that its vertices are chiral, with dextro and laevo forms alternating.

 
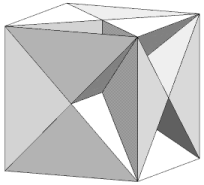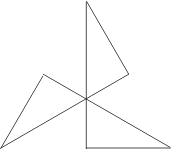Fig : Hemi faceted cube - 3D view and vertex figure

The reciprocal of the hemi faceted cube is an infinite stellation of the octahedron. I will call it an infinite octahedron. It has the appearance of six rhombic prisms, extending to infinity. Each face is bounded by three pairs of parallel edges, each from a different prism.

The traditional view is that the prisms extend to infinity in only one direction, which may be chosen arbitrarily. However, it is not possible to make a choice which both closes (i.e. fully bounds) the polyhedron and preserves both congruency of the infinite faces and symmetry of the polyhedron - conditions which the reciprocal must surely meet - so any such choice seems unacceptable.


Fig - Traditional mess

[3] presented an argument that a vertex at infinity has images in both directions. This provides the required closure, congruence and symmetry. It is unreasonable to treat different polyhedra differently on a whim, so all such prisms, reciprocal to any hemi faces, must have both ends.

In the centre of each infinite face is a triangular region, internal to all three pairs of prisms and having three vertices. At each of these vertices, three edges intersect - one from each pair. Each edge appears to be geometrically trisynaptic, having two finite vertices and a third at infinity along its length. This is untidy. The reciprocal vertex figure is both tidy and chiral, yet the geometric face appears to be neither. However, combinatorially each edge is connected to only one of the finite vertices. That is, a true vertex and a false vertex coincide. By disconnecting the correct edges, the trimethoric character is removed, and chirality restored. The edges and vertices are combinatorially tidy but appear geometrically untidy.


Fig - Face of the infinite octahedron

Chirality is generally treated as a geometric property, and not a combinatorial one. Yet we have seen that it does not appear to be preserved under reciprocation. How can this be? Either the form of chirality seen here is combinatorial in nature, or the meeting or missing of an edge passing through a vertex is a geometric property and not merely combinatorial. I have not yet figured the answer to this one. Possibly, this is because I do not understand the difference between projective and other kinds of geometry.

The reciprocal feature to the apparently trisynaptic edges is that along any edge of the original cube, three face planes (but not three faces) share a common line of intersection. We see the hemi solids as geometrically tidy, while their infinite reciprocals are untidy.

Holes and twists

When the Euler characteristics of different topological forms became apparent. Around 1900, Ludwig Schläfli argued that two of the Kepler-Poinsot stars were not proper polyhedra because they had the wrong Euler value and so were not equivalent to spheres in the way that convex polyhedra such as the Platonics are.

Elsewhere [3] I have mentioned the difficulty of allowing for certain kinds of hole in a polygon or polyhedron. A polygon essentially traces a circuit, which is not particularly useful here when things get complicated: holes can punch through overlapping circuits or loops and only really become significant when viewed from a higher dimension.

Holes are really just the flip side of filling the interior of a polygon or polyhedron. More about the importance of fillings can be found here.

Degenerate topologies

Candidates for degenerate polyhedra in Euclidean space include:

Tilings are sometimes seen as infinite polytopes, or apeirotopes, of higher dimension, having an infinite number of faces. For example plane tilings are apeirohedra. Certain non-planar arrangements also extend infinitely, dividing space into two parts. They are also apeirohedra, and have been variously called infinite polyhedra [Coxeter], honeycombs [], sponges [] and pseudopolyhedra [Gott]. How can they be polyhedra if they have no interior? Their structures conform to the definition of an abstract polytope, which allows infinite sets, but their maximal element is not realizable as any kind of interior. Because of this Johnson called them "improper" realizations, within the context of his own theory of "real" polytopes.

Any attempt to construct the regular star polyhedron {5/2 5/2} in Euclidean space goes on endlessly, with unpaired edges of polygons always present. It is in effect an infinite polyhedron much like a tiling, although it is tiling the sphere an infinite number of times rather than a flat plane only once.

But not all infinite polyhedra are degenerate. The Spidron polyhedra of Daniel Erdely have faces spiralling sequentially towards a certain vertex in ever-decreasing size, requiring an infinite number of ever-smaller faces to reach the vertex. Nevertheless the polyhedon conforms to abstract definitions and bounds a finite interior. These polyhedra are examples of where the abstract precursor is infinite but the realization is not. Hyperbolic tilings realized as a Poincaré disc provide further examples.

In many complicated self-intersecting figures, such as may be created through stellation, we can readily find examples where faces or vertices are visited by multiple circuits, or edges are visited twice by the same circuit or by different circuits. In certain situations, in a given surface n-space, we may find a compound or a composite where the figure divides up into structurally discrete but geometrically overlapping polyhedra. Such a compound is structurally degenerate, as it comprises multiple realizations of one or more abstract polytopes.

Some geometric figures may best be seen as n-methoric or n-synaptic forms, having n faces or vertices along a given edge. The structure of such figures breaks the dyadic rule, that only two (n-1)-topes meet along any (n-2) tope, so these figures are degenerate.

Abstract theory has recently thrown up another thorny issue. The definition of an abstract polyhedron (or polytope in higher dimensions) is simple, elegant and powerful. But it allows polytopes which are not simple n-spheres, such as projective polytopes. These figures are not amenable to the usual topological description as a CW-complex and are therefore topologically degenerate. Nevertheless, systematically identifying them at the theoretical level has proved extremely intractable and abstract theory is hardening into acceptance of them as valid polytopes. In my morphic theory I extend the principle down to polygons, allowing the interior to be for example a Môbius band. Such morphic polygons, and any polyhedra constructed from them, are also abstractly valid but topologically degenerate.

So even here, whether a given topology is tidy or untidy may depend on your area of interest.

Conclusion

I have previously suggested [3] that the dual or reciprocal of a tidy polyhedron should also be tidy. However, now that we have made the distinction between degeneracy and untidiness, we can say that while the dual of a degenerate structure will also be degenerate, the reciprocal of a tidy polyhedron may be tidy or untidy depending on the chosen projection (i.e. the chosen realisation and/or the chosen sphere of reciprocation).

Whe have seen how different geometrical figures can be classified according to their degree of degeneracy. For example the infinite "hemi duals" are combinatorially well-formed, and result from an accident of sphere location which has nothing to do with their underlying form. It is to be hoped that this classification will help bring some kind of order when asking of various figures, "is this a polyhedron or not, and if so then what kind is it?"

References

  1. N. Johnson; "Polytopes - abstract and real.
  2. J. Skilling;
  3. G. Inchbald, Towards stellating the icosahedron and faceting the dodecahedron , Symmetry: Culture and Science Vol. 14, 1-4 (2000) pp. 269-291.
  4. P. Pearce, Structure in nature is a strategy for design, MIT (1978).
  5. Gott; "Pseudopolyhedrons",.