Trimethoric (and Trisynaptic) Polyhedra
Updated 3 Apr 2023
This is an updated version of:
Inchbald, G.; "Trimethoric (and Trisynaptic) Polyhedra", Mathematics and Informatics Quarterly 2/2001, Volume 11, June 2001, pp.71-74.
Corrections and updates:
– Corrected the symbol for the pentagrammatic paraprisim.
– Origins as complex polyhedra added.
Abstract
Some polyhedral figures are described, with the peculiar properties that three faces meet along certain edges or three vertices occur on certain edges. They are examples of what have been called complex polyhedra. These threefold examples are here named trimethoric and trisynaptic polyhedra.
Introduction
As used here the term 'polyhedron' denotes a set of plane polygons forming a single closed (finite and unbounded) surface, 'face' denotes the entire area within a bounding polygon and 'region' denotes a part of a face which is bounded by edges or by lines of intersection with other faces and traversed by none.
This defintion is unusual in that it is not restricted to conventional polyhedra, which have by definition just two faces meeting at each edge, and just two vertices lying at the ends of eeach edge (e.g. [1]). Examples having more than two such faces at an edge or, correspondingly, more than two vertices along an edge, represent a generalisation of such polyhedra to surfaces which are not smooth (everywhere locally Euclidean) but bifurcated. They may have more than two faces meeting along an edge, or more than two vertices lying along an edge. They have occasionally been described as complex polyhedra. However this term nowadays implies the use of complex coordinates, so is not used here.
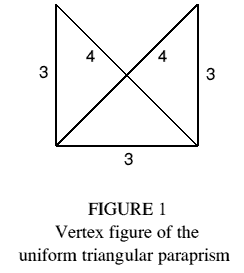
To see how three faces of a polyhedron can meet, we must consider its internal structure. If an internal region of a face meets two other mutually adjacent faces, along the same edge at which they already meet, then all three faces meet along this edge. The vertex figure of such a structure typically has the topology of Figure 1 (the vertex figure can be loosely thought of as the polygon formed by the cut edges when a vertex is sliced off; the number associated with each edge denotes the face which was cut, e.g. 3 denotes a triangle). The author is grateful for the suggestion of the term 'trimethoric' to describe such polyhedra (from the Greek methorion, an edge or boundary line). By contrast, conventional polyhedra may be termed 'bimethoric'.
Triangular paraprism
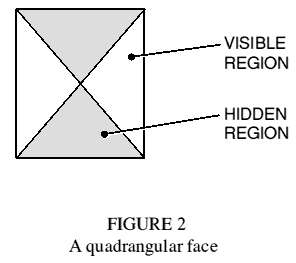
The general octahedron, comprising eight triangles, has three mutually intersecting quadrangles lying in its diagonal planes and passing through its centre. The octahedron is also a triangular antiprism. If the two end faces of the antiprism are removed, the diagonal quadrangles are partially exposed as new faces (Figure 2) and the polyhedron shown in Figure 3 results. It retains the external sides and symmetry of the parent antiprism, and the three rectangular faces (passing through its centre) are in like number to the rectangular sides of the associated (triangular) prism: I will call such polyhedra, with these prism properties but lacking end faces, 'paraprisms'.
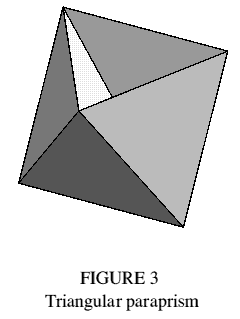
Because every edge where two triangular sides meet is also an edge of a quadrangle, the triangular paraprism is trimethoric. If derived from a regular octahedron, the triangular paraprism has regular faces and congruent vertices, and so is uniform: the vertex figure is shown in Figure 1.
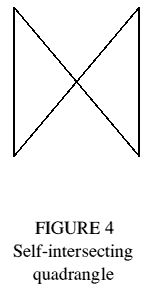
The exposed regions of the quadrangles could alternatively be thought of as bounded by self-intersecting quadrangular faces (Figure 4), as in Grünbaum [2]. In this case the structure is not trimethoric; and because it is not uniform it is quite distinct from the trimethoric polyhedron of the same visible external form. As Grünbaum points out, many different polyhedra can have the same visible external form.
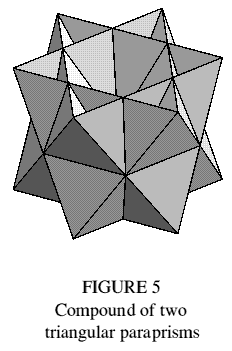
The compound of two triangular paraprisms shown in Figure 5, besides its aesthetic value, was incidentally the first trimethoric form recognised by the author.
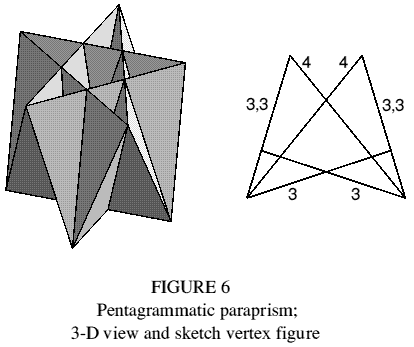
Pentagrammatic paraprism
No other antiprism has diagonal planes, but other paraprisms can be constructed using similar methods. For example, twist one pentagram of a pentagrammatic antiprism ( | 2 2 5/2 ) by 36° about the main axis. Twist a second antiprism the other way, then overlap the two in a compound such that their pentagrams are coincident and their triangular faces form overlapping coplanar pairs. This compound does have diagonal planes, so remove the pentagrams to expose them and obtain a pentagrammatic paraprism (figure 6). In the vertex figure, each side 3,3 represents a pair of coplanar triangles. The polyhedron is not uniform.
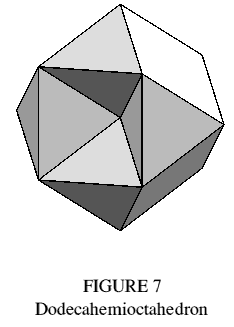
Dodecahemioctahedron
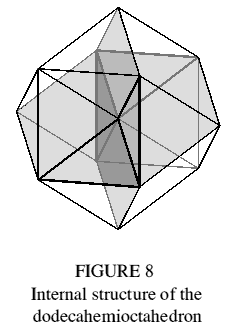
The dodecahemioctahedron is shown in Figure 7, and its internal structure in Figure 8. It may be derived from the cuboctahedron by inserting the four hexagons which lie in the latter's diagonal planes, and removing two opposing square faces. Triangular regions of the hexagons are now exposed, forming two dimples, while the remaining regions are internal and meet the outside surface at the edges joining square and triangular faces.
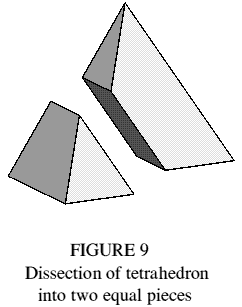
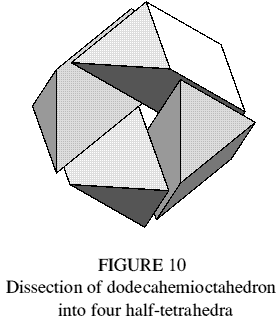
A common puzzle dissects the regular tetrahedron into two congruent pieces by making a cut across all four faces (Figure 9). The dodecahemioctahedron dissects into four such pieces (Figure 10). The figures show how a dodecahemioctahedron of side l can be dissected into two regular tetrahedra of side 2l. A space-filling variant with rhombic faces has been described [3], though its trimethoric nature was not recognised at the time; it should more correctly be named the rhombic dodecahemioctahedron.
Trimethoric rhombicuboctahedron
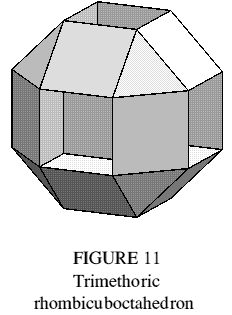
The edges of the rhombicuboctahedron define six octagons, lying in its diagonal planes. By removing the six square faces parallel to these planes (Figure 11), a trimethoric polyhedron is obtained. Like the triangular paraprism, its faces are regular and its vertices congruent. Unlike the polyhedra previously described, no faces pass through the centre; it therefore has a finite dual polyhedron, when reciprocated with respect to a sphere. The dual is straightforward to construct; it is outwardly similar to the compound of three Archimedean octagonal dipyramids and has three vertices (being reciprocal to the three faces of the original) incident at different points on a given edge: the description 'trisynaptic polyhedron' suggests itself.
Trimethoric icosahedra
The diagonal planes of the regular icosahedron form a great dodecahedron. By removing a set of 5, 10 or 15 symmetrically distributed triangular faces, three uniform trimethoric icosahedra are obtained. These have finite trisynaptic duals, all of similar outward appearance to the small stellated dodecahedron, which is dual to the great dodecahedron, but with differing internal structures.
Skilling's polyhedron
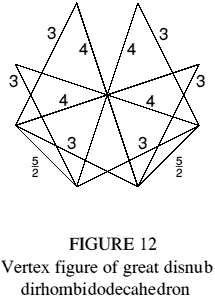
Skilling [4] describes a uniform polyhedron with up to four faces meeting at an edge. It is of interest here because it may be obtained in an alternative way, as a compound of 20 triangular paraprisms with 24 star pentagons attached to the trimethoric edges to render them 'tetramethoric'. This is illustrated via the vertex figure (Figure 12), which is seen to comprise the vertex figures of two triangular paraprisms (Figure 1), with the addition of two 5/2 sides connecting their trimethoric edges.
Two new classes of polyhedra
The faces of a polyhedron compound can characteristically be divided into closed subsets which are in themselves polyhedra. Although some closed subsets may be found for the trimethoric polyhedra described, in no case do all faces fall into distinct subsets. For example the triangular and hexagonal faces of the dodecahemioctahedron form an octahemioctahedron, but the square faces cannot be made part of an independent closed subset. So trimethoric polyhedra are not compounds of conventional polyhedra.
Several of the trimethoric polyhedra described are otherwise uniform. That is, they have regular faces and congruent vertices. A brief glance at the conventional (bimethoric) uniform polyhedra [5] indicates that many more must remain to be discovered. Intriguingly, Skilling [4] explicitly passes over at least one candidate vertex figure.
Trimethoric polyhedra are mathematically untidy, which is perhaps why they have not been recognised in the past. The ability of a conventional polyhedron's surface to close in a finite way around a defined internal space is associated with the ability to trace a circuit around any vertex figure. There is no obvious way to trace a circuit round a trimethoric vertex figure, yet these structures also appear to enclose a defined internal space in a finite way. Conventional polyhedra can be projected onto a continuous surface (a smooth manifold) such as a sphere or, in some cases, a more complicated but still continuous surface. Trimethoric forms can only be projected onto a discontinuous, bifurcated surface. Essentially the same principles also apply to trisynaptic polyhedra, since they are dual (i.e. inverse or reciprocal) to the trimethoric polyhedra.
As Cromwell [1] points out, the term "polyhedron" is used to describe many structures which do not meet conventional definitions. With the description "complex polyhedron" being restrcted to even less polyhedron-like objects, such as complex configurations, it seems appropriate to adopt the idea of trimethoric and trisynaptic, and in general n-methoric and n-synaptic, polyhedra. The examples described here have demonstrated the richness of these new classes of polyhedra, and the author hopes that this may prompt a more systematic and thorough treatment.
References
[1] P. Cromwell, Polyhedra, CUP (1997)
[2] B. Grünbaum, Polyhedra with hollow faces, Proc of NATO-ASI Conference on Polytopes ... etc. ... (Toronto 1993), ed T. Bisztriczky et al, Kluwer Academic (1994) pp. 43-70.
[3] G. Inchbald, Five space-filling polyhedra, Math. Gaz. 80 (November 1996) pp. 466-475.
[4] J. Skilling, The complete set of uniform polyhedra, Phil. Trans. 278 A (1975) pp. 111-135.
[5] H. S. M. Coxeter (et al), Uniform polyhedra, Phil. Trans. 246 A (1954) pp. 401-450.