Five Space-Filling Polyhedra

Updated 18 March 2019

This is by far my most popular web page, for some unknown reason. People seem to love my hendecahedra in their un-elongated forms and they are popular subjects for 3D printing. While you are here you might also like to explore my other polyhedron pages.

The text of this article is substantially reproduced by kind permission from:
Inchbald, G.; "Five Space-Filling Polyhedra", The Mathematical Gazette 80, November 1996, p.p. 466-475.

Various changes have been made from the original. The main ones are:

• Corrections to the coordinates of the sphenoid hendecahedron vertices A and L.
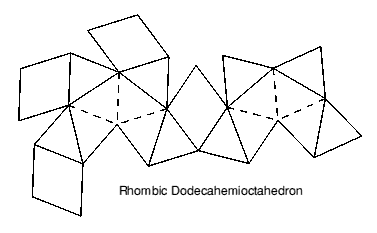
• The dodecahemioctahedron renamed as the rhombic dodecahemioctahedron, in order to distinguish it from the topologically similar polyhedron with regular faces. Correction to its description - the hexagons are not faces.
• The postscript on duality, cut from the original due to lack of space, is restored and updated.

Introduction

Solid shapes which pack together to fill space cover a large and varied range. I recently found five such polyhedra which I have not seen described elsewhere. The names which I have used for them here are rather ferocious I am afraid, but that just happens to be the way the names of polyhedra work.

Nets and coordinates for the polyhedra are given in Appendix A and Appendix B respectively.

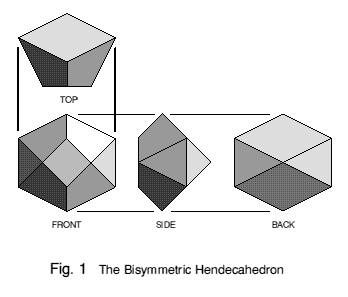
The bisymmetric hendecahedra

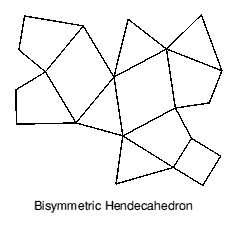
A polyhedron with eleven faces is called a hendecahedron, from the Greek for eleven. The one shown in Figure 1 has two planes of symmetry, i.e. it is bisymmetric. This hendecahedron also has eleven vertices; polyhedra with the same number of faces as vertices are not very common. It has 2 large rhombic faces, a small rhombic face (which in the proportions used here is square), 4 congruent iscosceles triangular faces which meet along edges at right angles, and 4 congruent kite-shaped faces. (see Appendix B for coordinates.)

Figures 2 and 3 shows how four hendecahedra together form a kind of hexagonal boat shape which will stack in interlocking layers. This boat shape is also a 'translation unit' - it can be regularly stacked in a lattice to fill space, without any rotation or reflection. This lattice is similar to the body-centred cubic, but scaled vertically by a factor which is here one-half (but see below). In Figure 4 the way the hendecahedra themselves stack together to form a space-filling 'honeycomb' can be seen.

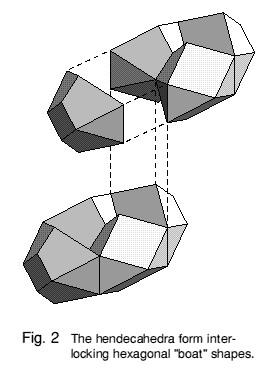
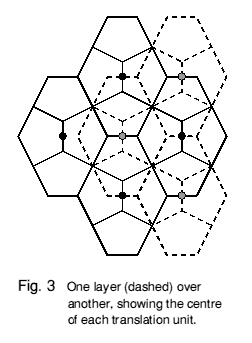
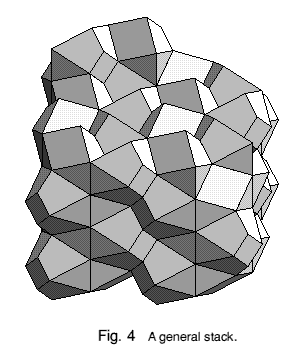
The particular polyhedron described here has an arbitrary height (chosen for convenience of its coordinates): it can be distorted vertically by stretching, to give an infinite series of shapes which are all space-fillers. In Figure 4, vertical lines can be seen running through the stack. Figure 2 shows how these lines are made from the edges where two triangular faces meet. In Figure 3, the lines are viewed end-on and appear as the corners where four hendecahedra from each layer meet. It is obvious from this that the angle between two triangular faces must be a right angle, but what should the other angles seen in Figure 3 be? These other angles can be varied by rotating the triangular faces together about their vertical edges, whilst maintaining the right angles and the overall symmetry of the shapes, up to the points at which faces merge or disappear. This rotation generates space-filling hendecahedra varying continuously from ones with broad front rhombs and blunt backs to ones with narrow front rhombs and sharper backs. The two distortions together yield a doubly-varying range of space-fillers.

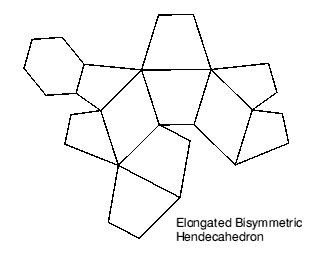
By cutting a hendecahedron in half horizontally and inserting a (pentagonal) prismatic centre section, an elongated bisymmetric hendecahedron is formed (Figure 5). The square face has become hexagonal, and the triangles are now trapezia (the term trapezium has two quite different interpretations - I use the term to describe a quadrilateral with one pair of parallel sides). The new solid has fourteen vertices with coordinates obtained from the original solid as described in Appendix B.

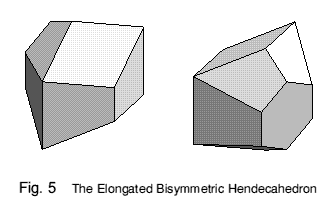
The shape fills space in a similar way to the unstretched variant. It may be distorted vertically in two independent zones: one being the prismatic centre zone and the other the tapering top and bottom ends corresponding to an unelongated shape. Together with rotation of the trapezoidal faces, this yields a threefold range of distortions which still fill space.

For a follow-up project based on this spacefilling, see:
Wu, Jiangmei and Inchbald, Guy; "Folding Space-Filling Bisymmetric Hendecahedron for a Large-Scale Art Installation", Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, 2018, Pages 483–486. (External link to PDF)

The sphenoid hendecahedra

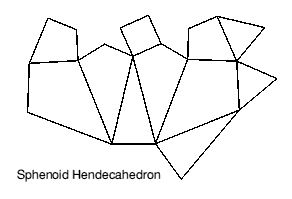
'Sphenoid' means wedge-shaped, which is an apt description for the hendecahedron shown in Figure 6. This also has eleven vertices, but it has only one plane of symmetry: top and bottom halves have reflective symmetry, but left and right halves are different, as can be seen in the end views. The sphenoid hendecahedron has three sizes of kite-shaped face and two types of isosceles triangle, all coming in pairs. In the proportions used here, the rhombic face is square. Unexpectedly the numbers of 3- and 4- sided faces are the same as for the bisymmetric variant, and indeed both hendecahedra have the same topology - they can be simply distorted into one another.

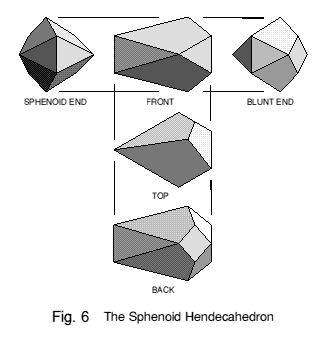
Figure 7 shows how six units pack like flower petals to form a 'floret'. A second floret fits up to it from below and is the other way up. The two florets form a translation unit which packs in a simple hexagonal lattice, here with a height equal to the unit length.

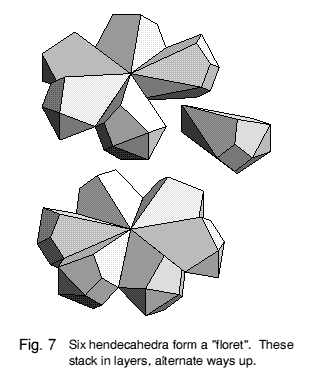
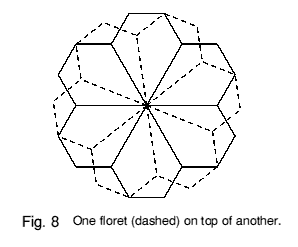
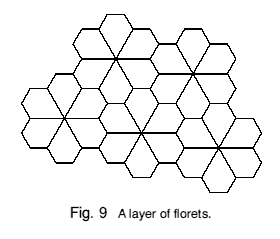
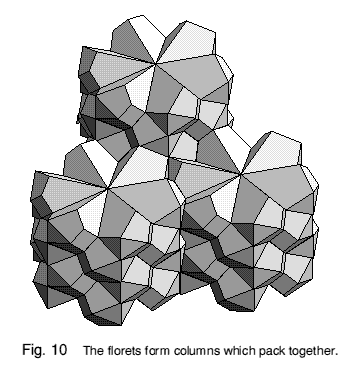
Florets will stack in layers, alternate ways up, to form faceted columns. In Figure 8, one floret is laid upon another, and in Figure 9 it can be seen how the florets also fit together side by side to form a layer. The layer is not quite symmetrical, alternate layers being right- and left-handed about the junction of three florets. Perhaps a little harder to visualise is the way the whole structure of layers and columns interlocks with no gaps, as illustrated in Figure 10.

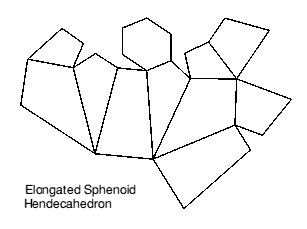
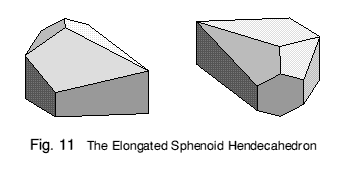
A new polyhedron can also be made by elongation (Figure 11): in the elongated sphenoid hendecahedron, the square face again becomes a hexagon and the triangles become trapezia. It also has fourteen vertices, with coordinates obtained from the original solid as described in Appendix B, and fills space in a similar way to its unstretched cousin.

The two sphenoid shapes can be distorted vertically in the same way as the bisymmetric ones, but have no analogue of the rotational distortion.

The rhombic dodecahemioctahedron

There are a number of solids with faces which pass through their centre, so that the face has no inside or outside but can be seen from both sides in different places. These central faces are typically parallel to the faces of some normal convex polyhedron, but number half as many. Figure 12 shows two of the four hexagonal face planes corresponding to half an octahedron which make this solid 'hemi-octa.' The hemi faces are the visible parts of the hexagons, and comprise 'butterfly' cross-quadrilaterals. Neither the hexagons nor the octahedron are regular, the octahedron being slightly flattened or 'oblate'. The solid also has 4 rhombic faces and 8 (isosceles) triangular ones, making in all 12 ordinary faces. Hence the name rhombic dodecahemioctahedron.

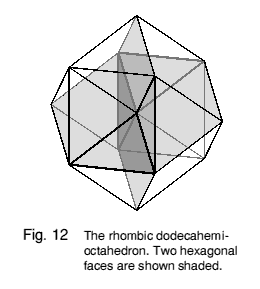
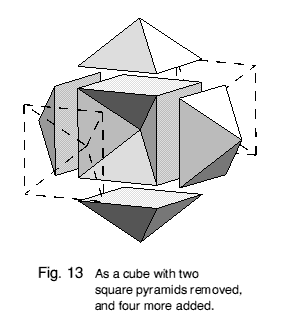
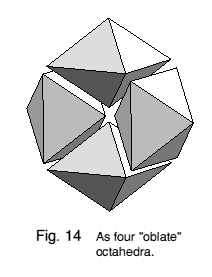
Figures 13 and 14 illustrate two other ways of deriving its shape: Figure 13 as a cube cut into six square pyramids meeting at the centre, with two opposing pyramids removed and four new pyramids stuck onto the square bases of the remaining ones, and Figure 14 as four oblate octahedra joined face to face around a central vertex. It can also be thought of as a rhombic dodecahedron with two oblate octahedra removed leaving dimples behind.

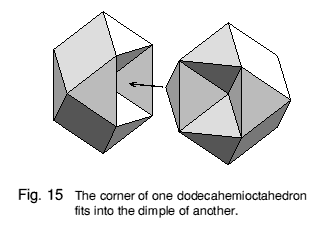
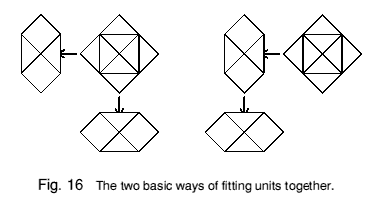
The corner of one rhombic dodecahemioctahedron exactly fits the dimple of another (Figure 15). A series of units can be fitted together in two basic ways, as in Figure 16. In various combinations, these give rise to several different packings which fill space. These packings are not true lattices, since they have 'false' edges, where the edge of one or more units lies across the face of another.

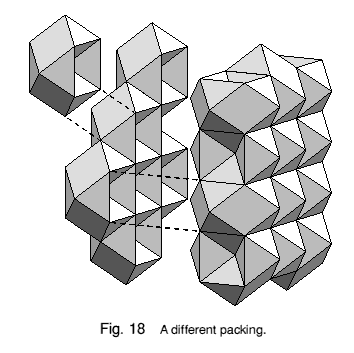
The most regular packing I have found is shown in Figure 17. The units form layers, each of which has alternate rows of peaks and dimples. The packing does not have full cubic symmetry, since the rows of peaks and dimples give each layer a directional 'grain'. But there is no distinction between the three main axes. Another packing, shown in Figure 18, forms distinct layers of peaks alternating with layers of dimples. This pattern is only seen in one plane, so the packing has a definite way up or orientation.

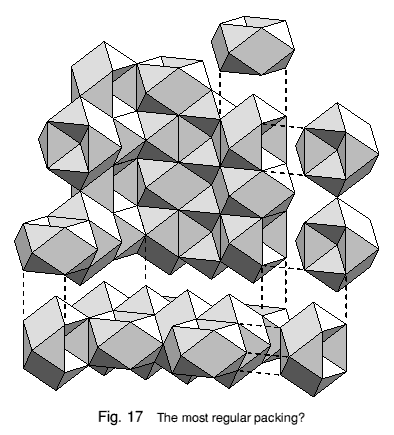
The rhombic dodecahemioctahedron is pristine, which means it cannot be distorted in any way and still fill space.

Postscript on duality

The reciprocal or dual of a polyhedron is a kind of anti-twin. It has vertices corresponding to the faces of the original, and faces to the vertices. It has the same number of edges as the original, but at right-angles to them. The relationship is reciprocal, which means that the dual of a dual is the original shape.

Self-dual polyhedra are possible: the regular tetrahedron is an example. Such a shape must have the same number of vertices as faces, and without going into detail the pattern, or topology, of edges around every face must corresond exactly to the pattern of edges meeting at every vertex. The two unelongated hendecahedra described share the same topology, which fulfils this requirement. But neither meets more subtle requirements for the angles of faces, etc. A self-dual hendecahedron does exist - it is the canonical form of this topology and is not a space-filler.

The rhombic dodecahemioctahedron does not have a finite dual. The dual feature corresponding to a face through the centre would be a vertex at infinity, in both opposing directions orthogonal to the face, therefore joining finite edges to it is not possible.

Acknowledgements

The 3-D views of polyhedra were created by WimpPoly and Polydraw software for the RISC OS (Acorn) operating system, from Fortran Friends, PO Box 64, Didcot, Oxon OX11 0TH. I am indebted to the author K. M. Crennell for advice, enthusiasm and pre-release software.

Appendix A: Nets

The elongated hendecahedra have slightly different z scalings from the given coordinates, but this should not matter for most purposes. Click to download printable copies.

Appendix B: Coordinates

Bisymmetric Hendecahedron

	x	y	z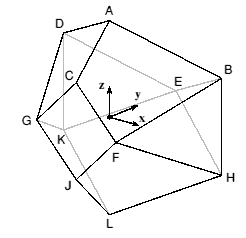
A:	0	0	2
B:	2	1	1
C:	0	-1	1
D:	-2	1	1
E:	0	2	0
F:	1	-1	0
G:	-1	-1	0
H:	2	1	-1
J:	0	-1	-1
K:	-2	1	-1
L:	0	0	-2

For an elongated version add ½ to the z ordinates of points A,B,C,D,E,F and G and subtract ½ from the z ordinates of points E,F,G,H,J,K and L, thus creating three additional vertices.

Sphenoid Hendecahedron

	x	y	z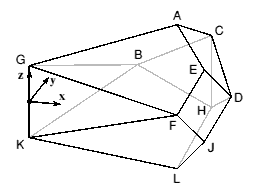
A:	13 / 7	3√3 / 7	1
B:	1	√3	0
C:	2	√3	0.5
D:	2.5	√3 / 2	0
E:	2.25	√3 / 4	0.5
F:	2	0	0
G:	0	0	0.5
H:	2	√3	-0.5
J:	2.25	√3 / 4	-0.5
K:	0	0	-0.5
L:	13 / 7	3√3 / 7	-1

For an elongated version add ½ to the z ordinates of points A,B,C,D,E,F and G and subtract ½ from the z ordinates of points B,D,F,H,J,K and L, thus creating three additional vertices.

Rhombic Dodecahemioctahedron

	x	y	z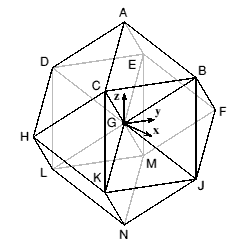
A:	0	0	2
B:	1	1	1
C:	1	-1	1
D:	-1	-1	1
E:	-1	1	1
F:	0	2	0
G:	0	0	0
H:	0	-2	0
J:	1	1	-1
K:	1	-1	-1
L:	-1	-1	-1
M:	-1	1	-1
N	0	0	-2